examples/io/external-viewers/polyscope/exampleGenericLatticeConvexHull4D.cpp

Computes the convex hull of N 4D points within a ball of radius R, these points belonging to a lattice of chosen dimension D. Displays their projections along the different main axes.

./examples/io/external-viewers/polyscope/exampleGenericLatticeConvexHull4D 20 100 2

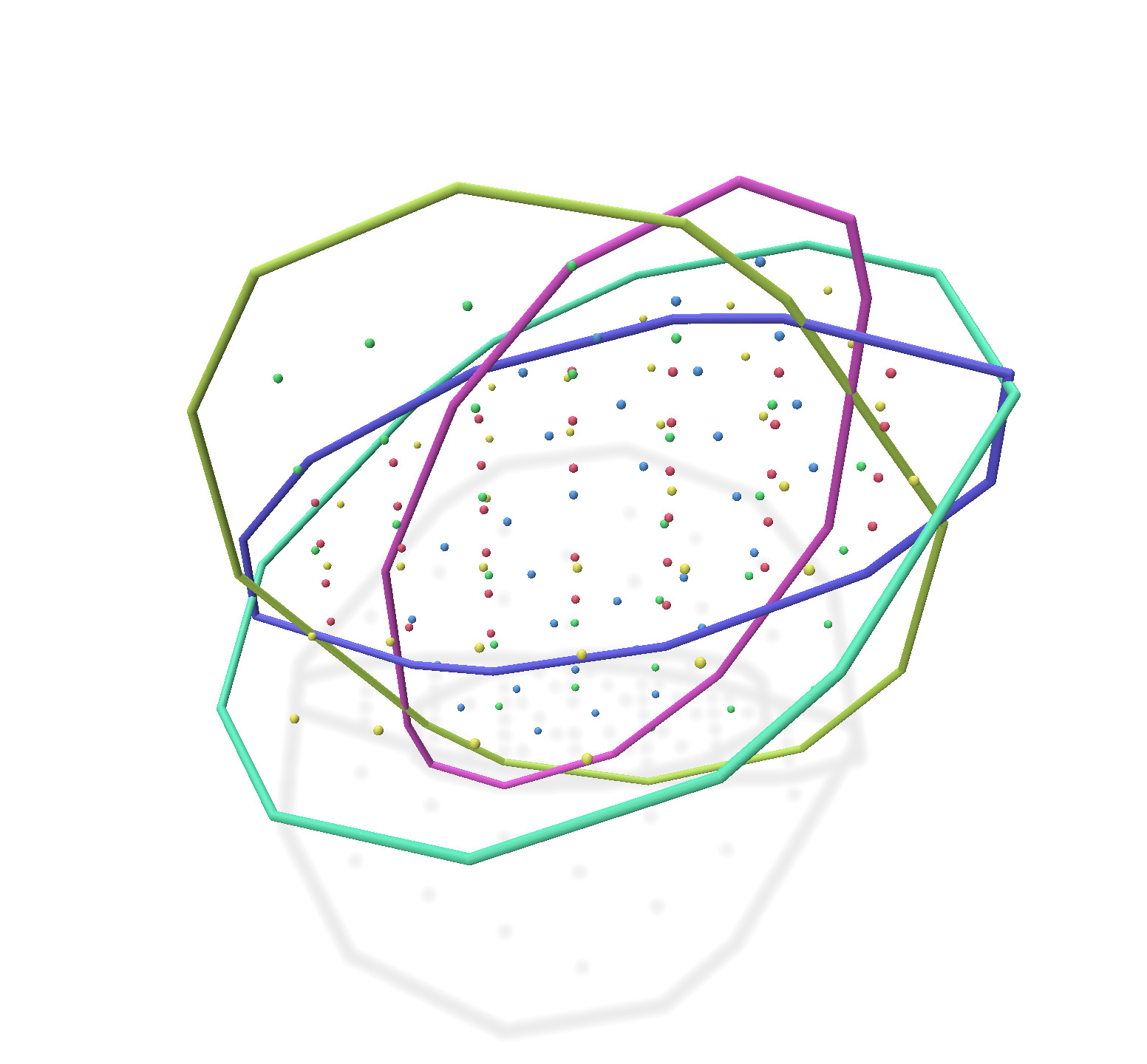
Convex hull of 100 4D points of affine dimension 2

See also

Further notes

 
#include <iostream>
#include <vector>
#include <random>
#include <algorithm>
#include <polyscope/polyscope.h>
#include <polyscope/surface_mesh.h>
#include <polyscope/point_cloud.h>
#include <polyscope/curve_network.h>
 
#include "DGtal/base/Common.h"
#include "DGtal/helpers/StdDefs.h"
#include "DGtal/geometry/tools/GenericLatticeConvexHull.h"
 
 
using namespace DGtal;
 
 
//Polyscope global
polyscope::PointCloud   *psPoints[4];
polyscope::PointCloud   *psVertices[4];
polyscope::PointCloud   *psBoundary0[4];
polyscope::CurveNetwork *psBoundary1[4];
polyscope::SurfaceMesh  *psBoundary2[4];
polyscope::Group        *group[4]; 
 
std::random_device rd;
std::mt19937 g(rd());
 
template < Dimension dim, typename TComponent, typename TContainer >
static
DGtal::PointVector< dim-1, TComponent, TContainer >
project( Dimension k,
         const DGtal::PointVector< dim, TComponent, TContainer >& p )
{
  DGtal::PointVector< dim-1, TComponent, TContainer > pp;
  Dimension l = 0;
  for ( Dimension i = 0; i < dim; i++ )
    if ( i != k )  pp[ l++ ] = p[ i ];
  return pp;
}
 
template < Dimension dim, typename TComponent, typename TContainer >
static
std::vector< DGtal::PointVector< dim-1, TComponent, TContainer > >
project( Dimension k,
         const std::vector< DGtal::PointVector< dim, TComponent, TContainer > >& V )
{
  std::vector< DGtal::PointVector< dim-1, TComponent, TContainer > > pV( V.size() );
  for ( auto i = 0; i < pV.size(); i++ )
    pV[ i ] = project( k, V[ i ] );
  return pV;
}
 
 
template < typename Point >
static
std::vector< Point >
makeRandomLatticePointsFromDirVectors( Point A, const std::vector< Point>& V,
                                       int nb, double radius, int amplitude, int aff_dim )
{
  std::uniform_int_distribution<int> U(-amplitude, amplitude);
  std::vector< Point > P;
  int m = std::min( aff_dim, (int) V.size() );
  for ( auto k = 0; P.size() < nb && k < 100000; k++ )
    {
      Point B = A;
      for ( auto i = 0; i < m; i++ )
        {
          int l = U( g );
          B += l * V[ i ];
        }
      if ( (B-A).norm() <= radius )
        P.push_back( B );
    }
  std::shuffle( P.begin(), P.end(), g );
  return P;
}
 
int main( int argc, char* argv[] )
{
  typedef GenericLatticeConvexHull< 4, int > QHull;
  typedef SpaceND< 4, int >                  Space;
  typedef Space::Point                       Point4;
 
  std::cout << "Usage: " << argv[ 0 ] << " [R=30] [N=30] [D=2]\n";
  std::cout << "Computes the convex hull of N 4D points within a ball of radius R, these points belonging to a lattice of chosen dimension 0<=D<=3. The output is projected along the 4 canonic projections onto 3D space. You cannot choose D=4 since we cannot diplay the result in 3D.\n";
  double radius = argc > 1 ? atof( argv[ 1 ] ) : 30.0;
  int    nb     = argc > 2 ? atoi( argv[ 2 ] ) : 30;
  int    adim   = argc > 3 ? atoi( argv[ 3 ] ) : 2;
  if ( nb < 0 ) return 1;
  if ( adim < 0 || adim > 3 ) return 1;
 
  // Create points
  std::vector< Point4 > L = { Point4{  4,  1, -3,  1 },
                              Point4{  0,  2,  5, -1 },
                              Point4{ -1, -3,  5,  0 },
                              Point4{  2,  0,  3, -3 } };
  std::vector< Point4 > X
    = makeRandomLatticePointsFromDirVectors( Point4(1,2,-1,0),
                                             L, nb,
                                             radius,
                                             int( round( radius+0.5 ) ),
                                             adim );
  
  // Compute convex hull
  QHull hull;
  bool ok = hull.compute( X );
  std:: cout << ( ok ? "[PASSED]" : "[FAILED]" ) << " hull=" << hull << "\n";
  // Initialize polyscope
  polyscope::init();
  std::string proj[ 4 ] = { "(yzw)", "(xzw)", "(xyw)", "(xyz)" };
  for ( Dimension k = 0; k < 4; k++ )
    {
      group     [k] = polyscope::createGroup( proj[k] );
      psPoints  [k] = polyscope::registerPointCloud( proj[k]+" Points",
                                                     project( k, X ) );
      psVertices[k] = polyscope::registerPointCloud( proj[k]+" Vertices",
                                                     project( k, hull.positions ) );
      psPoints  [k]->addToGroup( proj[k] ); // add by name
      psVertices[k]->addToGroup( proj[k] ); // add by name
 
      if ( hull.affine_dimension <= 1 ) // 1 or 2 points
        {
          // no facets
          psBoundary0[k] = polyscope::registerPointCloud( proj[k]+" Convex hull bdy dim=0",
                                                          project( k, hull.positions ) );
          psBoundary0[k]->addToGroup( proj[k] ); // add by name
        }
      else if ( hull.affine_dimension == 2 ) // 2D
        {
          // facets are edges (and implicitly converted by polyscope)
          psBoundary1[k] = polyscope::registerCurveNetwork( proj[k]+" Convex hull bdy dim=1",
                                                            project( k, hull.positions ),
                                                            hull.facets );
          psBoundary1[k]->addToGroup( proj[k] ); // add by name
        }
      else if ( hull.affine_dimension == 3 ) // 3D
        {
          // facets are polygons
          psBoundary2[k] = polyscope::registerSurfaceMesh( proj[k]+" Convex hull bdy dim=2",
                                                          project( k, hull.positions ),
                                                          hull.facets );
          psBoundary2[k]->addToGroup( proj[k] ); // add by name
        }
    }
  
  polyscope::show();
  return EXIT_SUCCESS;
  
}