Convex hull and alpha-shape in the plane

Table of Contents

• Convex hull
  • Andrew's algorithm
  • Graham's algorithm
  • Melkman's algorithm
  • Convex hull thickness
• Alpha-shape

Author(s) of this documentation:

Tristan Roussillon, Bertrand Kerautret

In this part of the manual, we describe how to compute well-known geometric structures such as the convex hull or the alpha-shape of a 2D point set. The proposed implementations provide exact results as long as the underlying geometric predicates are robust (see Implementation of geometric predicates for more details about geometric predicates).

Related examples are exampleConvexHull2D.cpp and exampleAlphaShape.cpp.

Convex hull

Let us recall that a polygon is a weakly externally visible polygon (WEVP) if for every point on it, there exists an infinite half-line beginning at this point, which does not intersect the polygon at anywhere else.

The two basic procedures functions::Hull2D::buildHullWithStack (the object having a stack interface is passed by reference) and functions::Hull2D::buildHullWithAdaptedStack (the object having a stack interface is passed by copy) retrieve the extremal vertices of a WEVP in linear-time. This is an implementation of a well-known method, called Sklansky's scan, Graham's scan or 3-coins algorithm, which has been proven to correctly retrieve the convex hull of any WEVP [Toussaint and Avis, 1982: [118]].

Three convex hull algorithms use this basic procedure:

• functions::Hull2D::andrewConvexHullAlgorithm [Andrew, 1979: [6]]
• functions::Hull2D::grahamConvexHullAlgorithm [Graham, 1972: [63]]
• functions::Hull2D::melkmanConvexHullAlgorithm [Melkman, 1987: [90]]

Before calling these algoritms, you must use the functions::Hull2D namespace defined in the file Hull2DHelpers.h.

#include "DGtal/geometry/tools/Hull2DHelpers.h"

  using namespace functions::Hull2D; 

Moreover, you need to create an orientation functor...

  typedef InHalfPlaneBySimple3x3Matrix<Z2i::Point, DGtal::int64_t> Functor;  
  Functor functor; 

... and, if required, a predicate

    typedef PredicateFromOrientationFunctor2<Functor, false, false> StrictPredicate; 
    StrictPredicate predicate( functor ); 

See Implementation of geometric predicates for more details about geometric predicates.

Note

The above functor returns:

• 0 for aligned points
• a strictly positive value for counter-clockwise oriented points
• a strictly negative value for clockwise oriented points

In this example, the predicate is an object that adapts the functor in order to return 'true' for striclty positive values. The last two template arguments means that neither the strictly negative values, nor the null values are accepted.

Andrew's algorithm

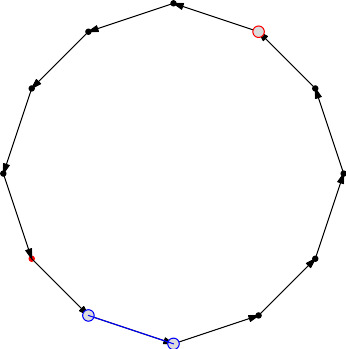
The more versatile algorithm is Andrew's one [Andrew, 1979: [6]], also known to be the monotone-chain algorithm. First, points are sorted along the horizontal axis. Then, the lower and upper convex hulls are computed by a simple Graham scan from left to right and from right to left. The resulting algorithm is correct because sorting points by increasing x-coordinates (and increasing y-coordinates for a same x-coordinate) produces a WEVP. The overall time complexity is \( O(n\log{(n)}) \) for a 2D point set of size \( n \).

Sorting step of Andrew's algorithm produces a WEVP

Note that the starting point is depicted in red and that the arrows show the point order.

In order to retrieve the extremal points of a range of points, you may call the procedure andrewConvexHullAlgorithm as follows:

    andrewConvexHullAlgorithm( pointSet.begin(), pointSet.end(), back_inserter( res ), predicate );   

Note that in this example the extremal points are pushed to a back insertion sequence called 'res'.

Convex hull of the digitization of a disk

You can however change the predicate to accept aligned points and therefore all points lying on the boundary of the convex hull.

    typedef PredicateFromOrientationFunctor2<Functor, false, true> LargePredicate; 
    LargePredicate predicate( functor ); 

All points lying on the boundary of the convex hull of the digitization of a disk

You can also change the predicate so that the resulting list of vertices is clockwise-oriented.

    typedef PredicateFromOrientationFunctor2<Functor, true, false> StrictPredicate; 
    StrictPredicate predicate( functor );

Clockwise-oriented list of extremal points of the digitization of a disk

Graham's algorithm

Graham's algorithm is another well-known algorithm to compute the convex hull of a 2D point set of size \( n \) in \( O(n\log{(n)}) \) [Graham, 1972: [63]]. The method can be coarsely described as follows:

• choose a pole and sort the points by increasing angle about the pole
• apply a simple Graham's scan on the sorted list of points.

We have chosen the point of maximal x-coordinate (and maximal y-coordinate) to be the pole. Hence, the algorithm is correct since sorting the points by increasing angle about such a pole produces again a WEVP.

Sorting step of Graham's algorithm produces a WEVP

The main advantage of Graham's algorithm over Andrew's one is that only one scan is required instead of two to retrieve the whole convex hull.

You may call the procedure grahamConvexHullAlgorithm as follows:

    grahamConvexHullAlgorithm( pointSet.begin(), pointSet.end(), back_inserter( res ), predicate ); 

Warning

You must choose a predicate returning 'true' for counter-clockwise oriented 3-point sets, because the sorting step is done with a counter-clockwise orientation.

Melkman's algorithm

The two previous algorithms are off-line and compute the convex hull of any set of \( n \) 2D points in \( O(n\log{(n)}) \).
Melkman's algorithm is on-line and computes the convex hull of a simple polygonal line, ie. without self-intersection, in linear-time (amortized constant time per update).

Note that Graham's scan, used by the two previous algorithms, runs in linear-time on weakly externally visible polygons, which is a subset of simple polygonal lines. As a consequence, Graham's scan may fail for simple polygonal lines that are not weakly externally visible.

In exampleConvexHull2D.cpp, you may find a minimal example:

A simple polygonal line that is not weakly externally visible

On such example, Graham's scan fails because the polygonal line is not weakly externally visible. However, Melkman's algorithm produces the right output:

Output for Melkman's algorithm

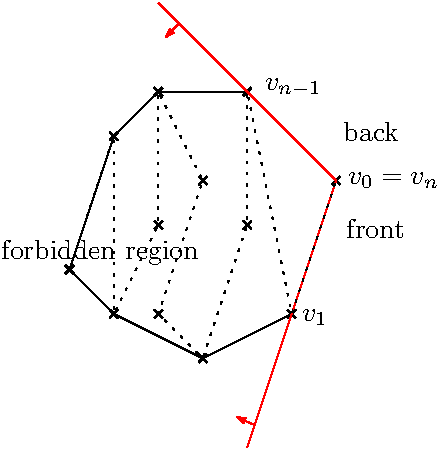
Melkman's algorithm works fine because it is based on a double ended queue and it
assumes that the input points form a simple polygonal line. Due to this assumption, any new point cannot be located in the cone formed by the first and last edge of the current convex hull (in red in the figure below). As a consequence, it is enough to update the convex hull by a Graham's scan from the front and/or from the back of the deque and it is never required to remove/insert points in the middle of the deque.

Consequence of the no self-intersection hypothesis

You may use MelkmanConvexHull class as follows:

    DGtal::MelkmanConvexHull<Z2i::Point, Functor> ch( functor ); 
    for (std::vector<Z2i::Point>::const_iterator 
           it = polygonalLine.begin(), 
           itEnd = polygonalLine.end(); 
         it != itEnd; ++it)
      ch.add( *it ); 

The class MelkmanConvexHull provides an on-line way of computing the convex hull of a sequence of points, which form a simple polygonal line: each time a point is added, the current convex hull is updated accordingly. However, if you are not interested in the on-line feature, you may call the off-line procedure melkmanConvexHullAlgorithm as follows:

    melkmanConvexHullAlgorithm( polygonalLine.begin(), polygonalLine.end(), back_inserter( res ), functor );   

Warning

The behavior is undefined if the input points do not form a simple polygonal line.

Constructing a Melkman convex hull from both sides.

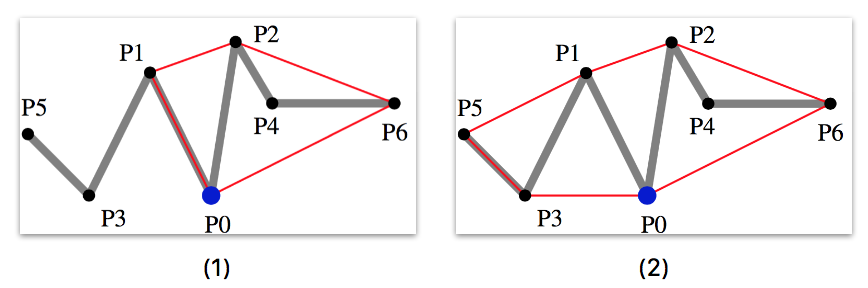
If you want to construction a convex hull by considering the front and back of a contour you will need to use the MelkmanConvexHull::reverse() method. For instance, to recover the convex hull of the point P0 of the following figure, you will need to do as follows:

typedef InHalfPlaneBySimple3x3Matrix<Z2i::RealPoint, double> Functor;
typedef MelkmanConvexHull<Z2i::RealPoint, Functor> MelkmanCV;
MelkmanCV ch;
ch.add(P0);
ch.add(P1);
ch.add(P2);
ch.reverse();
ch.add(P3);
ch.reverse();
ch.add(P4);
ch.reverse();
ch.add(P5);
ch.reverse();
ch.add(P6);

Such sequence will produce the correct result given on the image (2) of the following figure.

Illustration of the convex hull result starting from the point P0 and adding alternately the points Pi. (1) shows wrong convex hull obtained without the convex hull reverse, (2) is the correct convex hull obtained by using the reverse() method after each addition of points.

Convex hull thickness

From a convex hull it can be useful to compute its associated thickness. We propose the implementation of the well known rotating caliper algorithm allowing to compute all the antipodal pairs in linear time [Shamos , 1978: [113]].

Two definitions of thickness can be computed from an iterator on the convex hull. The first one is the vertical/horizontal thickness obtained by projection on the main x-y axis from antipodal pairs. The second one is given from the normal projection on the edge of the same antipodal pairs. The two definitions are illustrated on the following figures:

Example of the definitiion of horizontal/vertical thickness defined from the convex hull antipodal pair ((P,Q), S).

Example of the definitiion of Euclidean thickness defined from the convex hull antipodal pair ((P,Q), S).

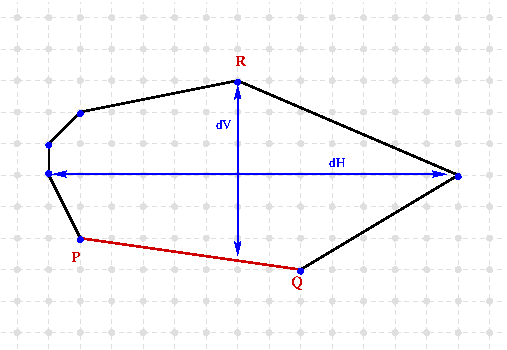
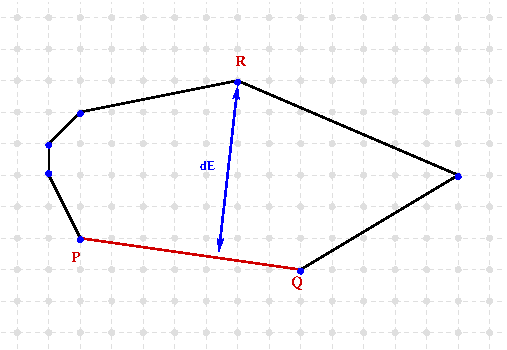
To compute the thickness of a convex hull you have simply to call the computeHullThickness procedure:

    double th = DGtal::functions::Hull2D::computeHullThickness(res.begin(), res.end(), DGtal::functions::Hull2D::HorizontalVerticalThickness);

To recover the antipodal pairs for which the thickness is minimal you can also use the same method with an antipodal pair:

    Z2i::Point antipodalP, antipodalQ, antipodalS;
    th = DGtal::functions::Hull2D::computeHullThickness(res.begin(), res.end(), DGtal::functions::Hull2D::HorizontalVerticalThickness, antipodalP, antipodalQ, antipodalS);

And display the result:

    board.setPenColor(DGtal::Color::Red);
    board.drawCircle( antipodalS[0], antipodalS[1], 0.2) ;
    board.setPenColor(DGtal::Color::Blue);
    board.drawCircle(antipodalP[0], antipodalP[1], 0.2);
    board.drawCircle(antipodalQ[0], antipodalQ[1], 0.2);
    board.drawLine(antipodalP[0], antipodalP[1], antipodalQ[0], antipodalQ[1]);

By using the sequence of points of the first example, you will obtain a thickness of 12 with the following antipodal pair:

Example of antipodal pair obtained from the computation of the horizontal/vertical thickness. The edge (P, Q) of the antipodal pair is represented in blue and its vertex R is given in red.

Warning

The convex hull should be oriented in counter clockwise else it will return wrong result.

Alpha-shape

The alpha-shape of a finite set of points has been introduced in [Edelsbrunner et. al., 1983: [50]]. This geometric structure is based on the following concept of generalized disk.
For an arbitrary real \( \alpha \), a generalized disk of radius \( 1/\alpha \) is defined as

• a disk of radius \( 1/\alpha \) if \( \alpha > 0 \)
• a complement of the disk of radius \( -1/\alpha \) if \( \alpha < 0 \)
• a half-plane if \( \alpha = 0 \)

We also define the direct (resp. indirect) generalized disk of radius \( 1/\alpha \) passing by two points \( P \) and \( Q \) as the unique generalized disk of radius \( 1/\alpha \) with \( P, Q \) on its boundary and such that \( P, Q \) and its center are counter-clockwise oriented (resp. clockwise oriented).

The \(\alpha\)-hull of a point set is the intersection of all closed generalized disks of radius \( 1/\alpha \) that contains the point set. A point \( P \) of this point set is \(\alpha\)-extreme if there exists a closed generalized disk of radius \( 1/\alpha \) such that \( P \) lies on its boundary and which contains all the other points.
The \(\alpha\)-shape is the straight-line graph whose vertices are the \(\alpha\)-extreme points and whose edges connect any two \(\alpha\)-extreme points such that there exists a closed generalized disk of radius \( 1/\alpha \) with both points on its boundary and which contains all the other points.

Any \(\alpha\)-shape of a set of points is a subgraph of either the closest point or the farthest point Delaunay triangulation. Moreover, the set of \(\alpha_1\)-extreme points is a subset of the set of \(\alpha_2\)-extreme points if \(\alpha_1 \geq \alpha_2 \).

Various \(\alpha\)-shapes of the digitization of a disk are depicted below for \( \alpha \in \{ -1, -1/\sqrt{5}, -1/5, 0, 1/9, 1/8 \} \).

alpha = -1 (8-connected boundary)

alpha = -0.4472

alpha = -0.2 (points lying on the boundary of the convex hull)

alpha = 0 (convex hull)

alpha = 0.1111

alpha = 0.125 (points lying on the smallest enclosing circle)

You may observe that:

• if \( \alpha = -1 \), we retrieve the 8-connected boundary
• if \( \alpha = -\epsilon \) for an arbitrary small \( \epsilon \), we retrieve all the points lying on the boundary of the convex hull
• if \( \alpha = 0 \), we retrieve the convex hull vertices.
• if the radius of the smallest enclosing circle is denoted by \( R_{min} \), we retrieve all the points lying on the smallest enclosing circle if \( \alpha = 1/R_{min}-\epsilon \) for an arbitrary small \( \epsilon \).

Even if the convex hull of a set of points is its \(0\)-shape, the following properties are not true for general \(\alpha\)-shapes, \( \alpha \neq 0 \):

• The \(\alpha\)-shape of 3 points always exists and is always connected,
• For any 3-point set \( P, Q, R \) in the plane,
  if \( R \) belongs to the direct generalized disk of radius \( 1/\alpha \) passing by \( P \) and \( Q \) then \( P \) belongs to the direct generalized disk of radius \( 1/\alpha \) passing by \( Q \) and \( R \) and \( Q \) belongs to the direct generalized disk of radius \( 1/\alpha \) passing by \( R \) and \( P \).

As a consequence, the current implementation cannot compute the alpha-shape of an arbitrary set of points. Such an algorithm would have required to compute the closest point and farthest point Delaunay triangulation. Though, we provide procedures, based on the 3-coins algorithm, which compute in linear-time the alpha-shape of specific polygons, for which the two above properties remain true: closedGrahamScanFromVertex (the starting point is expected to be extremal) and closedGrahamScanFromAnyPoint (no assumption about the starting point is required).

This class of polygons is the set of simple polygons such that:

• The distance between any two consecutive vertices is smaller than \( 2/\alpha \) if \( \alpha > 0 \) or greater than \( -2/\alpha \) if \( \alpha < 0 \). This guarantees that the \(\alpha\)-shape of three consecutive vertices always exists (if \( \alpha > 0 \)) and is always connected (if \( \alpha < 0 \)).
• For every set of three consecutive vertices \( P, Q, R \) of the polygon, \( PR \) is the longest side of the triangle \( P, Q, R \).

Let us consider a connected and convex digital object such that its 4-connected (resp. 8-connected) boundary is simply 4-connected (resp. 8-connected). It is clear that its 4-connected (resp. 8-connected) boundary belongs to the above class of polygons provided that \( -1 \leq \alpha < 1/R_{min} \) (resp. \( -\sqrt{2}/2 \leq \alpha < 1/R_{min} \)). We can therefore compute any alpha-shape of the digitization of a compact and convex set by a linear-time scan of the points of its boundary.

In such cases, you can perform the computation in two steps. First, you must define a predicate from an instance of InGeneralizedDiskOfGivenRadius as follows:

    typedef AvnaimEtAl2x2DetSignComputer<DGtal::int64_t> DetComputer; 
    typedef InGeneralizedDiskOfGivenRadius<Z2i::Point, DetComputer> Functor; 
    Functor functor(true, 1, 0); //alpha = 0; 1/alpha -> +inf 
    typedef PredicateFromOrientationFunctor2<Functor> Predicate; 
    Predicate predicate( functor ); 

Then, you can call the procedure closedGrahamScanFromAnyPoint as follows:

    closedGrahamScanFromAnyPoint( border.begin(), border.end(), back_inserter( res ), predicate );   

In order to create an instance of InGeneralizedDiskOfGivenRadius, you must provide the value of \( 1/\alpha \) by three arguments:

• a boolean to set the sign of \( \alpha \) ('true' if \( \alpha \geq 0 \), 'false' if \( \alpha < 0 \)),
• the squared numerator of \( 1/\alpha \)
• the squared denominator of \( 1/\alpha \). As shown above, \( \alpha = 0 \) if this third argument is zero.
  

For example, the following line set \( \alpha \) to \( 1/9 \).

    Functor functor(true, 81, 1); //1/alpha = sqrt(81/1) = 9 

The above illustrations are generated by the program written in exampleAlphaShape.cpp.