The following programs are related to this documentation: geometry/surfaces/examplePlaneProbingTetrahedronEstimator.cpp, geometry/surfaces/examplePlaneProbingParallelepipedEstimator.cpp, geometry/surfaces/examplePlaneProbingSurfaceLocalEstimator.cpp, testDigitalPlanePredicate.cpp, testPlaneProbingTetrahedronEstimator.cpp, testPlaneProbingParallelepipedEstimator.cpp.

Introduction to plane-probing algorithms

A plane-probing algorithm (see [73], [106], [77] and [87]) computes the normal vector of a set of digital points from a starting point and a predicate InPlane: "Is a point x in the set of digital points?". This predicate is used to probe the set as locally as possible and decide on-the-fly the next points to consider, in order to deform a particular set of points, which is tangent by construction. The growth direction is given by both arithmetic and geometric properties. The main characteristics of these algorithms is that no parameter is required for the analysis of the local geometry of digital surfaces. Furthermore, they present theoretical guarantees, most notably they extract the exact normal vector of any digital plane.

Tetrahedron-based probing methods

The first kind of plane-probing algorithms is based on the deformation of a tetrahedron. The objective of the algorithm is to iteratively update one vertex of this tetrahedron until one of its faces is parallel to the digital set. The update procedure will consist in selecting a point inside a candidate set. Multiple candidate sets have been proposed but we will start by describing the simplest one, the so-called H-neighborhood. We start by illustrating its behavior when the digital set is a digital plane segment. The next image shows the initial state of the estimator. We will denote by \( (v_k)_{0 \leq k \leq 2 } \) the three vertices of the base triangle (the blue disks on the left), \( q \) a fixed point outside the set at the top of the tetrahedron (the blue circle). Points that are inside the digital set will be denoted by disks while points that are outside by circles.

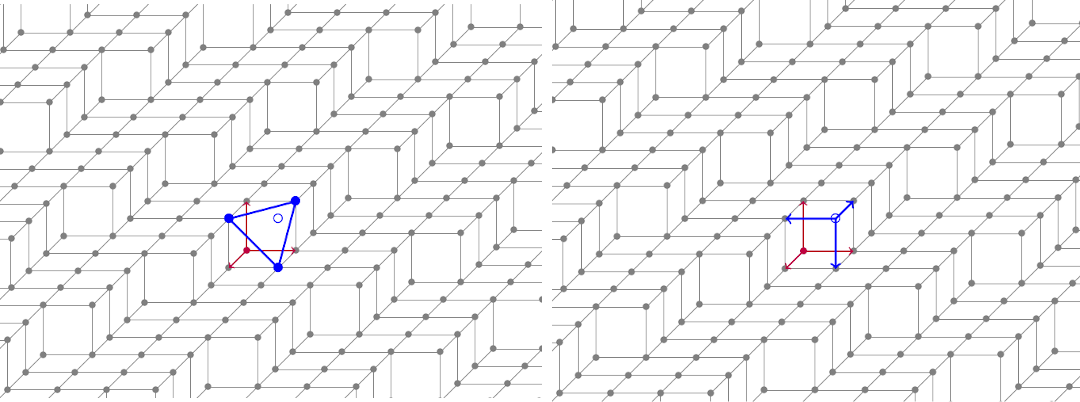
Left: the base triangle. Right: the base frame at the begining.

We now describe the update procedure in more details, see the next figure.

From left to right: before the update, H-neighborhood in red, filtering through InPlane, closest criterion, after the update

At a given iteration, the update step consists of the following substeps:

computing the candidate set (in red),
filtering through the InPlane predicate,
selecting the closest one according to some criterion (here we use a simple Delaunay/InSphere one),
updating one vertex of the base triangle.

The algorithm stops whether one of the following criteria is verified:

the candidate set does not contain a point inside the digital set,
the current configuration of the H-neighborhood is non-convex,
the current configuration of the H-neighborhood is non-planar. For the last two, see [73] or the enum PlaneProbingNeighborhood::HexagonState for more details.

Other candidate sets were proposed namely the R-neighborhood [73] and an optimization that we call R1-neighborhood [77]. The main difference is that instead of considering 6 points of an hexagon, they consider 6 rays. This allows to reduce the number of steps and to obtain a reduced basis at the end. We recommend to use the R1-neighborhood.

The main drawback of this category of algorithms is the fact that they return the correct normal vector on a digital plane only when starting from specific points (precisely reentrant corners of low height). In all other cases, the estimated normal is only an approximation. In the next section, we will present another kind of estimator that can be initialized on any surfel of a digital surface and which returns the correct normal on every surfel of a digital plane.

Parallelpiped-based probing methods

The second kind of plane-probing algorithms is based on the deformation of a pair of tetrahedra i.e. a parallelepiped introduced in [77]. The parallelepiped is ensured to always be separating (one point is always inside the digital set and one point always outside). This approach allows to start the algorithm on any surfel (at least 4 points inside the digital set) and is more general than the previous one.

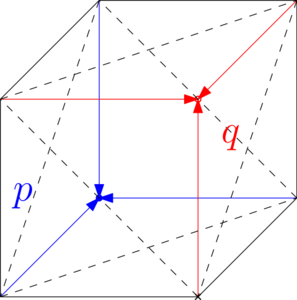
The two tetrahedra are displayed in red and blue. The points p and q are the bases of the two tetrahedra.

This approach is internally based on a new predicate NotAbove that is able to tell whether a digital point \( x \) has a height that is smaller or greater than the one of \( q \). It is easy to see that it can be implemented using ray-casting and the InPlane predicate. It naturally increases the number of calls to InPlane but has several advantages. See [77] or this presentation (in French) for more details.

We will denote by PH, PR and PR1 the three variations of the parallelepiped estimator for the three different candidate sets.

Summary of the different variants

Algorithm	Principle	Initialization	Candidate Set
H	Downward oriented tetrahedron	Any reentrant corner	6 points in a hexagon
R, R1	Downward oriented tetrahedron	Any reentrant corner	6 points + 6 rays
PH	Separating parallelepiped	Any point	6 points in a hexagon
PR, PR1	Separating parallelepiped	Any point	6 points + 6 rays

Constructing and using a plane-probing estimator

General method

In DGtal, both categories of plane-probing estimators are implemented, see PlaneProbingTetrahedronEstimator for the first category and PlaneProbingParallelepipedEstimator for the second one. In the following, we explain the API for PlaneProbingTetrahedronEstimator.

The general way of instantiating a plane-probing estimator is the following:

  // The general form is ProbingEstimator<Predicate, mode> where
  // - Predicate is a model of concepts::PointPredicate, see DigitalPlanePredicate or DigitalSurfacePredicate for instance,
  // - mode specifies the candidate set, it is one of { ProbingMode::H, ProbingMode::R, ProbingMode::R1, ProbingMode::L }.
  using DigitalPlane = DigitalPlanePredicate<Space>;
  using Estimator    = PlaneProbingTetrahedronEstimator<DigitalPlane, ProbingMode::R1>;
 
  // We start by constructing the predicate, here a standard digital plane of normal (2, 6, 15)
  Vector n(2, 6, 15);
  DigitalPlane plane(n, 0, n.norm1());
 
  // Instantiation: estimator(startingPoint, initialFrame, predicate) where
  // (startingPoint, initialFrame) describes the initial tetrahedron.
  Point o(0, 0, 0);
  std::array<Point, 3> m = { Point(1, 0, 0), Point(0, 1, 0), Point(0, 0, 1) };
  Estimator estimator(o, m, plane);

And to use it:

  int it = 0;
  while (estimator.advance().first) {
      it++;
 
      // You can examine the current configuration of the H-neighborhood, using PlaneProbingTetrahedronEstimator::hexagonState
      auto state = estimator.hexagonState();
      if (state == Estimator::Neighborhood::HexagonState::Planar) {
          std::cout << "Planar" << std::endl;
      } else if (state == Estimator::Neighborhood::HexagonState::Empty) {
          std::cout << "Empty" << std::endl;
      } else if (state == Estimator::Neighborhood::HexagonState::NonPlanar) {
          std::cout << "NonPlanar" << std::endl;
      } else if (state == Estimator::Neighborhood::HexagonState::NonConvex) {
          std::cout << "NonConvex" << std::endl;
      }
 
      // Here, we display the current frame (the vectors m_k) and the current estimation
      std::clog << "it = " << it << " "
          << estimator.m(0) << " " << estimator.m(1) << " " << estimator.m(2) << " "
          << estimator.getNormal() << std::endl;
  }
 
  // This loop can also be reduced to:
  // Point n = estimator.compute()

The common services shared by plane-probing estimators are the following:

PlaneProbingTetrahedronEstimator::m returns the three vectors \( (m_k)_{0 \leq k \leq 2} \) defining the tetrahedron.
PlaneProbingTetrahedronEstimator::q returns the fixed point \( q \).
PlaneProbingTetrahedronEstimator::getOrigin returns the base point of the frame \( q - (m_0 + m_1 + m_2) \).
PlaneProbingTetrahedronEstimator::vertices returns the three vertices \( (q - m_k)_{0 \leq k \leq 2} \).
PlaneProbingTetrahedronEstimator::hexagonState returns the current configuration of the H-neighborhood.

Probing services:

PlaneProbingTetrahedronEstimator::advance does one step of the estimation.
PlaneProbingTetrahedronEstimator::compute repeatedly calls advance until a final configuration is found.
PlaneProbingTetrahedronEstimator::getBasis returns the two shortest edges of the base triangle.
PlaneProbingTetrahedronEstimator::isReduced tells whether the vectors returned by getBasis form a reduced basis or not.
PlaneProbingTetrahedronEstimator::getNormal returns the current normal vector.

Services specific to PlaneProbingParallelepipedEstimator :

PlaneProbingParallelepipedEstimator::getState returns the number of points that are inside the digital set according to InPlane.
PlaneProbingParallelepipedEstimator::isSeparating returns a boolean testing whether the current parallelepiped is separating or not.
PlaneProbingParallelepipedEstimator::isInReverseState returns a boolean saying whether the current parallelepiped is in a reverse state or not.

On a digital surface

The PlaneProbingDigitalSurfaceLocalEstimator adapter can use any plane-probing estimator class to estimate normals on a digital surface. It is a model of concepts::CSurfelLocalEstimator and concepts::CDigitalSurfaceLocalEstimator.

The definition and instantiation is done as follows:

    using SurfacePredicate = DigitalSurfacePredicate<Surface>;
    using ProbingAlgorithm = PlaneProbingParallelepipedEstimator<SurfacePredicate, ProbingMode::R1>;
    // The general form is PlaneProbingDigitalSurfaceLocalEstimator<SurfaceType, ProbingAlgorithm>
    using Estimator        = PlaneProbingDigitalSurfaceLocalEstimator<Surface, ProbingAlgorithm>;
 
    // Parameters of the estimator:
    // - the probing factory
    Estimator::ProbingFactory probingFactory = [&bound](const Estimator::ProbingFrame& frame, const SurfacePredicate& surfacePredicate) {
        // If the base estimator is a PlaneProbingTetrahedronEstimator
        // return new ProbingAlgorithm(frame.p, { frame.b1, frame.b2, frame.normal }, surfacePredicate);
 
        // For a PlaneProbingParallelepipedEstimator
        return new ProbingAlgorithm(frame.p, { frame.b1, frame.b2, frame.normal }, surfacePredicate, bound);
    };
 
    // - an optional hashmap of pre-estimations
    std::unordered_map<Surfel, RealPoint> preEstimations;
    // The user can provide the pre-estimation
    // auto preEstimationsVector = SHG3::getCTrivialNormalVectors(surface, surfels, params);
    // for (std::size_t i = 0; i < surfels.size(); ++i)
    // {
    //     preEstimations[surfels[i]] = preEstimationsVector[i];
    // }
    // Or if it is not given, it is implicitly done inside the Estimator::eval function (using the MaximalSegmentSliceEstimation estimator)
 
    // - a verbosity flag
    bool verbose = true;
 
    Estimator estimator(surface, probingFactory, preEstimations, verbose);
    estimator.init(gridstep, surfels.begin(), surfels.end());

And to use it:

    // Evaluation on a range of surfels
    std::vector<Estimator::Quantity> quantities;
    estimator.eval(surfels.begin(), surfels.end(), std::back_inserter(quantities));
 
    // Or on one surfel 's'
    // Estimator::Quantity q = estiamtor.eval(s);

Warning: Due to its nature, PlaneProbingTetrahedronEstimator only returns an approximation of the normal vector on every surfel that is not a reentrant corner. If you want to have a correct estimation on every surfel, use a PlaneProbingParallelepipedEstimator instead as the base.

The parameters that are specific to this estimator are the following:

the probing factory is a function that takes as input a frame (a base point and three vectors) and a reference to the predicate. It should return a dynamically allocated plane-probing estimator from these inputs.
pre-estimations. Due to its nature, a plane-probing algorithm only works correctly in the octant determined by the initial frame. If this octant is not correct, then the estimated normal will also be incorrect. That is why we use so-called pre-estimations that must be normal vectors that are cheap to evaluate and that are used to construct a good initial frame. The user can provide such estimations via the third parameter, otherwise it is automatically computed internally using a MaximalSegmentSliceEstimation estimator.

Model of concepts::CSurfelLocalEstimator :