topology/cubical-complex-collapse.cpp

Collapse of 3D cubical complex that is made of 20x20x20 voxels with their faces. Fixed cells were marked in red. It was the eight vertices, plus all border linels on the upper faces plus a random linel within the complex. The priority was the distance to the diagonal. Note that the Euler characteristic of the complex is unchanged after collapse.

See also

Topological operations: closing, opening, collapsing a complex

* $ ./examples/topology/cubical-complex-collapse
* New Block [Creating Cubical Complex]
*   After close: [CubicalComplex dim=3 chi=1 #0=9261 #1=26460 #2=25200 #3=8000]
* EndBlock [Creating Cubical Complex] (12.088 ms)
* New Block [Collapsing complex]
* [CC::collapse]-+ tag collapsible elements...    68756 found.
* [CC::collapse]-+ entering collapsing loop. 
* [CC::collapse]---+ Pass 1, Card(PQ)=68921 elements, nb_exam=0
* [CC::collapse]---+ Pass 2, Card(PQ)=16219 elements, nb_exam=68921
* [CC::collapse]---+ Pass 3, Card(PQ)=7956 elements, nb_exam=85140
* [CC::collapse]---+ Pass 4, Card(PQ)=36 elements, nb_exam=93096
* [CC::collapse]-+ cleaning complex.
* Collapse removed 64066 cells.
* After collapse: [CubicalComplex dim=2 chi=1 #0=1268 #1=2427 #2=1160 #3=0]
* EndBlock [Collapsing complex] (162.069 ms)
* $
* 

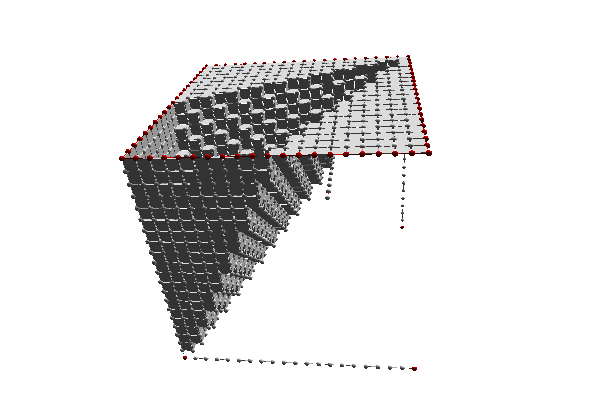
Collapse of a cubical complex made of 20x20x20 voxels with some cells marked as fixed (in red).

 
#include <iostream>
#include <map>
#include "DGtal/base/Common.h"
#include "DGtal/helpers/StdDefs.h"
 
#include "DGtal/io/viewers/PolyscopeViewer.h"
#include "DGtal/topology/KhalimskySpaceND.h"
#include "DGtal/topology/CubicalComplex.h"
 
 
using namespace std;
using namespace DGtal;
using namespace DGtal::Z3i;
 
 
template <typename CubicalComplex>
struct DiagonalPriority {
  typedef typename CubicalComplex::KSpace KSpace;
  typedef typename CubicalComplex::Point  Point;
  typedef typename CubicalComplex::Cell   Cell;
  typedef typename CubicalComplex::CellMapIterator CellMapIterator;
  
  DiagonalPriority( const CubicalComplex& complex ) : myComplex( complex ) {}
  bool operator()( const CellMapIterator& it1, const CellMapIterator& it2 ) const
  {
    Point k1 = myComplex.space().uKCoords( it1->first );
    Point k2 = myComplex.space().uKCoords( it2->first );
    double d1 = Point::diagonal( 1 ).dot( k1 ) / sqrt( (double) KSpace::dimension );
    double d2 = Point::diagonal( 1 ).dot( k2 ) / sqrt( (double) KSpace::dimension );;
    RealPoint v1( k1[ 0 ] - d1 * k1[ 0 ], k1[ 1 ] - d1 * k1[ 1 ], k1[ 2 ] - d1 * k1[ 2 ] );
    RealPoint v2( k2[ 0 ] - d2 * k2[ 0 ], k2[ 1 ] - d2 * k2[ 1 ], k2[ 2 ] - d2 * k2[ 2 ] );
    double n1 = v1.dot( v1 );
    double n2 = v2.dot( v2 );
    return ( n1 < n2 ) || ( ( n1 == n2 ) && ( it1->first < it2->first ) );
  }
  
  const CubicalComplex& myComplex;
};
 
int main( int argc, char** argv )
{
  // JOL: unordered_map is approximately twice faster than map for
  // collapsing.
  typedef std::map<Cell, CubicalCellData> Map;
  // typedef boost::unordered_map<Cell, CubicalCellData>   Map;
  typedef CubicalComplex< KSpace, Map >     CC;
 
  trace.beginBlock( "Creating Cubical Complex" );
  KSpace K;
  K.init( Point( 0,0,0 ), Point( 512,512,512 ), true );
  CC complex( K );
  Integer m = 40;
  std::vector<Cell> S;
  for ( Integer x = 0; x <= m; ++x )
    for ( Integer y = 0; y <= m; ++y )
      for ( Integer z = 0; z <= m; ++z )
        {
          Point k1 = Point( x, y, z ); 
          S.push_back( K.uCell( k1 ) );
          double d1 = Point::diagonal( 1 ).dot( k1 ) / (double) KSpace::dimension; // sqrt( (double) KSpace::dimension );
          RealPoint v1( k1[ 0 ], k1[ 1 ], k1[ 2 ] );
          v1 -= d1 * RealPoint::diagonal( 1.0 );
          //RealPoint v1( k1[ 0 ] - d1 * k1[ 0 ], k1[ 1 ] - d1 * k1[ 1 ], k1[ 2 ] - d1 * k1[ 2 ] );
          double n1 = v1.norm();
          bool fixed = ( ( x == 0 ) && ( y == 0 ) && ( z == 0 ) )
            || ( ( x == 0 ) && ( y == m ) && ( z == 0 ) )
            || ( ( x == m ) && ( y == 0 ) && ( z == 0 ) )
            || ( ( x == m ) && ( y == m ) && ( z == 0 ) )
            || ( ( x == m/3 ) && ( y == 2*m/3 ) && ( z == 2*m/3 ) )
            || ( ( x == 0 ) && ( y == 0 ) && ( z == m ) )
            || ( ( x == 0 ) && ( y == m ) && ( z == m ) )
            || ( ( x == m ) && ( y == 0 ) && ( z == m ) )
            || ( ( x == m ) && ( y == m ) && ( z == m ) )
            || ( ( x == 0 ) && ( y == m ) )
            || ( ( x == m ) && ( y == m ) )
            || ( ( z == 0 ) && ( y == m ) )
            || ( ( z == m ) && ( y == m ) );
          complex.insertCell( S.back(), 
                              fixed ? CC::FIXED 
                              : (DGtal::uint32_t) floor(64.0 * n1 ) // This is the priority for collapse 
                              );
        }
  //complex.close();
  trace.info() << "After close: " << complex << std::endl;
  trace.endBlock();
 
  // for 3D display with PolyscopeViewer
  typedef PolyscopeViewer<Space, KSpace> MyViewer;
 
  {
    MyViewer viewer(K);
    typedef CC::CellMapConstIterator CellMapConstIterator;
    for ( Dimension d = 0; d <= 3; ++d )
      for ( CellMapConstIterator it = complex.begin( d ), itE = complex.end( d );
            it != itE; ++it )
        {
          bool fixed = (it->second.data == CC::FIXED);
          if ( fixed ) viewer.drawColor( Color::Red );
          else         viewer.drawColor( Color::White );
          viewer << it->first;
        }
    viewer.show();
  }
  
  trace.beginBlock( "Collapsing complex" );
  CC::DefaultCellMapIteratorPriority P;
  DGtal::uint64_t removed 
    = functions::collapse( complex, S.begin(), S.end(), P, true, true, true );
  trace.info() << "Collapse removed " << removed << " cells." << std::endl;
  trace.info() << "After collapse: " << complex << std::endl;
  trace.endBlock();
 
  {
    MyViewer viewer(K);
    typedef CC::CellMapConstIterator CellMapConstIterator;
    for ( Dimension d = 0; d <= 3; ++d )
      for ( CellMapConstIterator it = complex.begin( d ), itE = complex.end( d );
            it != itE; ++it )
        {
          bool fixed = (it->second.data == CC::FIXED);
          if ( fixed ) viewer.drawColor( Color::Red );
          else         viewer.drawColor( Color::White );
          viewer << it->first;
        }
    viewer.show();
    return 0;
  }
}