Mesh Voxelization

Table of Contents

• Introduction
• Basic Usage
• Limitations

Author(s) of this documentation:

David Coeurjolly, Monir Hadji

See also

DGtalTools MeshVoxelizer

Introduction

This documentation describes a voxelization approach of a triangulated structure. The proposed approach follows the method described by Laine [78].

Note

The digitization is not a solid voxelization in the sense that if the input mesh is a closed surface, interior voxels are not exported. Only the triangles are digitized.

The approach is rather simple: Given a triangulated mesh, the MeshVoxlizer processes each triangle independently. If the triangle intersects a given template centered at a given grid point, then the grid point belongs to the digitization of the triangle.

The geometry of the template is used to control the topology of the resulting digital set. We provide two templates to obtain 6- and 26-separable digital sets (see Limitations for discussion).

Template for 6-separating digitization

Template for 26-separating digitization

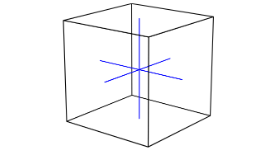
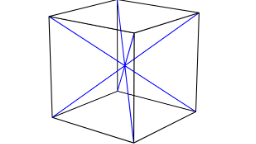
Basic Usage

Given a Mesh aMesh, the MeshVoxelizer class is templated by a type of digital set (model of concepts::CDigitalSet) to store the voxels, and an integer specifying the expected separability of the surface (either 6 or 26).

Let us first create a simple unit cube (see exampleMeshVoxelizer)

  using namespace Z3i;
  Mesh<Point> aMesh;
 
  trace.info()<<"Creating a cube"<<std::endl;
  //Creating a cube
  aMesh.addVertex(Point(0,0,0));
  aMesh.addVertex(Point(1,0,0));
  aMesh.addVertex(Point(1,1,0));
  aMesh.addVertex(Point(0,1,0));
  aMesh.addVertex(Point(0,1,1));
  aMesh.addVertex(Point(1,1,1));
  aMesh.addVertex(Point(1,0,1));
  aMesh.addVertex(Point(0,0,1));
  
  aMesh.addQuadFace(0,1,2,3);
  aMesh.addQuadFace(1,2,5,6);
  aMesh.addQuadFace(7,6,5,4);
  aMesh.addQuadFace(3,2,5,4);
  aMesh.addQuadFace(0,3,4,7);
  aMesh.addQuadFace(0,1,6,7);

We first include the class:

#include "DGtal/shapes/MeshVoxelizer.h"

We then create a voxelization of a scaled version of the cube onto a \( 128^3\) domain:

  Domain domain(Point(0,0,0), Point(128,128,128));
  DigitalSet outputSet(domain);
  
  MeshVoxelizer<DigitalSet, 6> voxelizer;
 
  trace.info()<<"Digitization..."<<std::endl;
  voxelizer.voxelize(outputSet, aMesh, 15.0);
 
  trace.info()<<"Got "<< outputSet.size() << " voxels."<<std::endl;

Once exported

  Board3D<> board;
  for(auto voxel : outputSet)
    board << voxel;
  board.saveOBJ("voxelizedCube.obj");

we obtain the following voxel set:

Resulting voxelSet (quad faces triangulated by the viewer)

Note

If you have enabled OpenMP in DGtal, the voxelizer will perform the digitization of the triangles in parallel.

Warning

If the input mesh has non-triangular faces, such faces will be automatically triangulated using a naive fan approach. Hence, if the face in not planar and/or convex, the resulting digitization might be incorrect.

Here you have another example with a more complex mesh (using DGtaltools tools for visualization):

Voxelization at different resolutions of a Stanford Bunny.

Limitations

At this point intersection tests are performed using arithmetics on double as an approximation of \( \mathbb{R}^3\). The digitization may not be exact when the mesh are integer or rational vertices for instance.