Tutorial "Image -> Region -> Grid curve -> Length estimation"

Table of Contents

• Extracting a digital set from an image
• Extracting the contours of a digital set
• Grid curve instantiation
• Length estimation
• Required includes

Author(s) of this documentation:

Tristan Roussillon

In this example, we show how to retrieve the contour of a connected subset of an image and estimate its perimeter.

Extracting a digital set from an image

Let us assume that the following image has been loaded into an image object:

S gray level image

First of all, we implicitely extract a digital set from an image, using a simple threshold on gray level values:

  //predicate from the image
  typedef DGtal::functors::IntervalThresholder<Image::Value> Binarizer;
  Binarizer b(1, 135); 
  PointFunctorPredicate<Image,Binarizer> predicate(image, b); 

Note

The explicit construction of the digital set is not necessary.
Since the domain of the image is known (methods lowerBound() and upperBound()), it is indeed enough to have a predicate that indicates, for each point of the domain, whether it belongs to the digital set or not.

This predicate returns true for each dark pixel of the following image:

S binary image

Extracting the contours of a digital set

The extraction of the contour is performed in a cellular space (with 0-, 1-, and 2-cells), given an adjacency (0-, 1-, 2-adjacency). See Cellular grid space and topology, unoriented and oriented cells, incidence for the basic concepts of cellular topology.

  Z2i::KSpace ks;                                            //Khalimsky space 
  ks.init( image.domain().lowerBound(), image.domain().upperBound(), true );
  SurfelAdjacency<2> sAdj( true );                           //adjacency

Then, the contour of each connected component can be retrieved as follows:

  //extraction of all the contours
  std::vector< std::vector< Z2i::SCell > > contours;
  Surfaces<Z2i::KSpace>
    ::extractAll2DSCellContours( contours, ks, sAdj, predicate );

Grid curve instantiation

The GridCurve object is merely built from one retrieved contour, which is stored as a vector of signed 1-cells:

    //init grid curve from the first retrieved contour
    Z2i::Curve c;
    c.initFromSCellsVector( contours.at(1) );  

Length estimation

Now, we want to get a perimeter estimation of the grid curve c. Several length estimators have been implemented in DGtal, but we are using in what follows the one based on a greedy segmentation of the curve into digital straight segments (DSS).

Since the DSS recognition algoritm deals with digital points, we get the points range of the grid curve c.

    //range of points
    typedef Z2i::Curve::PointsRange Range; 
    Range r = c.getPointsRange(); 

The DSS segmentation looks like this:

DSS segmentation

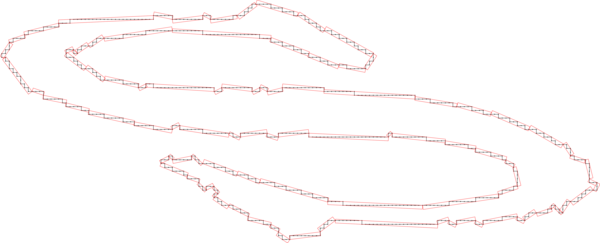
Then, we initialize the DSS length estimator from the points range and get the estimated length.

    //length estimation based on a DSS segmentation
    DSSLengthEstimator< Range::ConstCirculator > DSSlength;
    trace.info() << "Length: " << DSSlength.eval(r.c(), r.c(), 1.) << std::endl; 

You should see in the standard output:

Length: 723.238 

Required includes

You should include these common files:

#include "DGtal/base/Common.h"
#include "DGtal/helpers/StdDefs.h"
#include "ConfigExamples.h"

For loading the image and extracting a digital set by thresholding:

#include "DGtal/base/BasicFunctors.h"
#include "DGtal/kernel/BasicPointPredicates.h"
#include "DGtal/io/readers/PGMReader.h"
#include "DGtal/images/ImageContainerBySTLVector.h"

For extracting the contours of the digital set:

#include "DGtal/topology/helpers/Surfaces.h"

And finally, for estimating the length of the retrieved contours, you should include this:

#include "DGtal/geometry/curves/estimation/DSSLengthEstimator.h"