Generator Tools

2dSimplePolygonDigitizer

The digitizer compute the set of integer points inside the input polyline.Usage: 2dSimplePolygonDigitizer [input] [output]Allowed options are:

Positionals:
1 TEXT:FILE REQUIRED                  Input polyline filename (sdp).
 
Options:
 
Positionals:
1 TEXT:FILE REQUIRED                  Input polyline file name.
 
Options:
-h,--help                             Print this help message and exit
-i,--input TEXT:FILE REQUIRED         Input sdp filename.
-o,--output TEXT=result.pgm           the output image filename (pgm or svg)

Example:

$2dSimplePolygonDigitizer -i ${DGtal}/tests/samples/flower-30-8-3.sdp -o sample.pgm

You will obtain such image:

Resulting image

Example with more complex contours: The file located in $DGtal/examples/samples/contourS.sdp

$ 2dSimplePolygonDigitizer -i  $DGtal/examples/samples/contourS.sdp -o sample2.pgm

You will obtain such image:

Resulting image

See also

2dSimplePolygonDigitizer 2dSimplePolygonDigitizer.cpp

3dParametricCurveDigitizer

Usage: 3dParametricCurveDigitizer [options] –curve <curve> –param1 <double> –param2 <double> –param3 <double> –tstart <double> –tend <double> –step <double> –output <basename>Allowed options are:

-h,--help                             Print this help message and exit
--param1 FLOAT=1                      a radius or a scaling factor (default 0)
--param2 FLOAT=1                      a radius or a scaling factor (default 0)
--param3 FLOAT=1                      a radius or a scaling factor (default 0)
--tstart FLOAT                        start time
--tend FLOAT                          end time
-s,--step FLOAT                       step
-k,--knext UINT=5                     K_NEXT value (default 5)
-l,--list                             List all available shapes
-c,--curve TEXT                       Shape name
-a,--angle FLOAT=0                    Rotation angle in radians(default 0)
--ox FLOAT=0                          X coordinate of origin (default 0)
--oy FLOAT=0                          Y coordinate of origin (default 0)
--oz FLOAT=0                          Z coordinate of origin (default 0)
--ax FLOAT=1                          X component of rotation axis (default 1)
--ay FLOAT=0                          Y component of rotation axis (default 0)
--az FLOAT=0                          Z component of rotation axis (default 0)
-o,--output TEXT                      Basename of the output file

You can list the potential curves:

$ 3dParametricCurveDigitizer --list
3D Parametric curves:
       EllipticHelix Helix with two axes and a distance between consecutive turns. Its period is 2 * Pi.
        Required parameter(s): --param1, --param2, --param3
       Knot_3_1 Parametric knot 3_1 i.e., a trefoli polynomial knot
        Required parameter(s): --param1, --param2, --param3
       Knot_3_2 Parametric knot 3_2 i.e., a trefoli knot having a period of 2 * Pi
        Required parameter(s): --param1, --param2, --param3
       Knot_4_1 Parametric knot 4_1 (polynomial knot)
        Required parameter(s): --param1, --param2, --param3
       Knot_4_3 Parametric knot 4_3 having a period 2 * Pi.
        Required parameter(s): --param1, --param2, --param3
       Knot_5_1 Parametric knot 5_1 (polynomial knot)
        Required parameter(s): --param1, --param2, --param3
       Knot_5_2 Parametric knot 5_2 having a period 2 * Pi
        Required parameter(s): --param1, --param2, --param3
       Knot_6_2 Parametric knot 6_2 (polynomial knot)
        Required parameter(s): --param1, --param2, --param3
       Knot_7_4 Parametric knot 7_4 (polynomial knot)
        Required parameter(s): --param1, --param2, --param3

Example:

# generate a trefoli knot:
3dParametricCurveDigitizer --curve Knot_3_1 --param1 10 --param2 10 --param3 10 --tstart -2.2 --tend 2.2 --step 0.001 --output knot_3_1

See also

3dParametricCurveDigitizer.cpp 3dParametricCurveDigitizer

contourGenerator

The associated geometric information like contour, curvature can also be displayed.Usage: contourGenerator –shape <shapeName> [requiredParam] [otherOptions]Allowed options are:

-h,--help                             Print this help message and exit
-l,--list                             List all available shapes
-s,--shape TEXT                       Shape name
-R,--radius FLOAT                     Radius of the shape
-A,--axis1 FLOAT                      Half big axis of the shape (ellipse)
-a,--axis2 FLOAT                      Half small axis of the shape (ellipse)
-r,--smallradius FLOAT=5              Small radius of the shape (default 5)
-v,--varsmallradius FLOAT=5           Variable small radius of the shape (default 5)
-k UINT=3                             Number of branches or corners the shape (default 3)
--phi FLOAT=0                         Phase of the shape (in radian, default 0.0)
-w,--width FLOAT=10                   Width of the shape (default 10.0)
-p,--power FLOAT=2                    Power of the metric (default 2.0)
-x,--center_x FLOAT=0                 x-coordinate of the shape center (default 0.0)
-y,--center_y FLOAT=0                 y-coordinate of the shape center (default 0.0)
-g,--gridstep FLOAT=1                 Gridstep for the digitization (default 1.0)
-f,--format TEXT=pts                  Output format:
                                          List of pointel coordinates {pts}
                                          Freeman chaincode Vector {fc} (default pts)
-o,--outputGeometry TEXT              Base name of the file containing the shape geometry (points, tangents, curvature)

You can also list all possible shapes:

contourGenerator --list
2D Shapes:
       ball    Ball for the Euclidean metric.
               Required parameter(s): --radius [-R]
       square  square (no signature).
               Required parameter(s): --width [-w]
       lpball  Ball for the l_power metric (no signature).
               Required parameter(s): --radius [-R], --power [-p]
       flower  Flower with k petals with radius ranging from R+/-v.
               Required parameter(s): --radius [-R], --varsmallradius [-v], --k [-k], --phi
       ngon    Regular k-gon.
               Required parameter(s): --radius [-R], --k [-k], --phi 
       accflower       Accelerated Flower with k petals.
               Required parameter(s): --radius [-R], --varsmallradius [-v], --k [-k], --phi
       ellipse Ellipse.
               Required parameter(s): --axis1 [-A], --axis2 [-a], --phi 

Example:

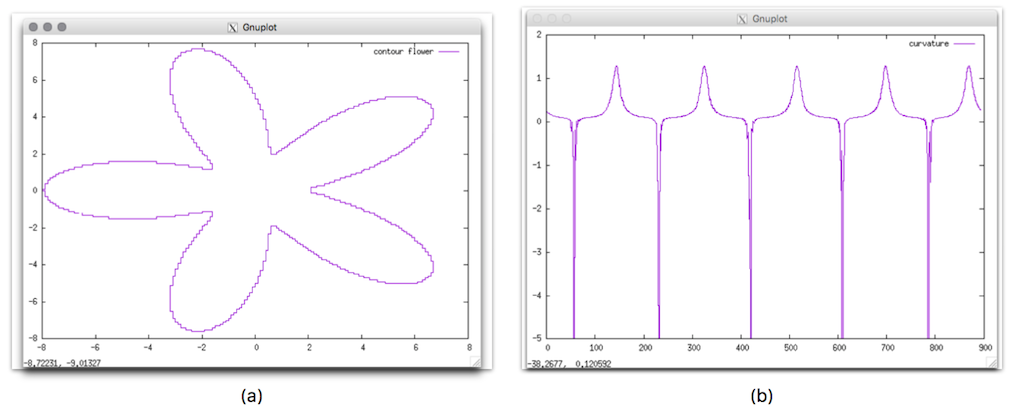
# generate a flower contour with 5 petals of maximal radius 5 and small radius 3 with grid size = 0.1:
./shapeGenerator/contourGenerator -s flower -R 5 -v 3 -k 5 --outputGeometry result -g 0.1
# Display the results using gnuplot:
$gnuplot
[gnuplot> plot [][-5:2]'res.geom' using 1:6 w l t "curvature"
[gnuplot> plot 'res.geom' using 2:3 w l t "contour flower"

You should obtain such a visualization:

resulting visualisation of generated contour (a) and curvature (b).

See also

contourGenerator.cpp shapeGenerator

shapeGenerator

Usage: shapeGenerator [options] –shape <shapeName> –output <outputBasename>Allowed options are:

-h,--help                             Print this help message and exit
-l,--list                             List all available shapes
-s,--shape TEXT                       Shape name
-R,--radius FLOAT                     Radius of the shape
-A,--axis1 FLOAT                      Half big axis of the shape (ellipse)
-a,--axis2 FLOAT                      Half small axis of the shape (ellipse)
-r,--smallradius FLOAT=5              Small radius of the shape (default 5)
-v,--varsmallradius FLOAT=5           Variable small radius of the shape (default 5)
-k UINT=3                             Number of branches or corners the shape (default 3)
--phi FLOAT=0                         Phase of the shape (in radian, default 0.0)
-w,--width FLOAT=10                   Width of the shape (default 10.0)
-p,--power FLOAT=2                    Power of the metric (default 2.0)
-o,--output TEXT                      Basename of the output file
--signature                           Display to the standard output the signature (normal, curvature) at each point of the specified shape contour (middle point of each contour linel)
-f,--format TEXT                      Output format:
                                          Bitmap {pgm, raw}
                                          Vector {svg} (+ {png,pdf} if libCairo installed) (default pgm)

You can list the potential shapes:

$ contourGenerator --list
2D Shapes:
       ball     Ball for the Euclidean metric.
        Required parameter(s): --radius [-R]
       square   square (no signature).
        Required parameter(s): --width [-w]
       lpball   Ball for the l_power metric (no signature).
        Required parameter(s): --radius [-R], --power [-p]
       flower   Flower with k petals with radius ranging from R+/-v.
        Required parameter(s): --radius [-R], --varsmallradius [-v], --k [-k], --phi
       ngon     Regular k-gon.
        Required parameter(s): --radius [-R], --k [-k], --phi
       accflower        Accelerated Flower with k petals.
        Required parameter(s): --radius [-R], --varsmallradius [-v], --k [-k], --phi
       ellipse  Ellipse.
        Required parameter(s): --axis1 [-A], --axis2 [-a], --phi

Example:

# generate an accflower shape with 6 petals of maximal radius 40 and small radius 10:
shapeGenerator -s accflower -R 40 -v 10 -k 6   -f pgm  -o test2

You should obtain such a resulting image:

resulting visualisation of generated shape.

See also

shapeGenerator.cpp contourGenerator