Table of Contents
- Author(s) of this documentation:
- Jacques-Olivier Lachaud
- Since
- 1.3
Part of the Geometry package.
This part of the manual describes some applications of a new definition of digital convexity, called full convexity [80] [81] .
See Digital convexity, full convexity and P-convexity for further details on full convexity.
See Fully convex envelope, relative fully convex envelope and digital polyhedra to see how to build fully convex hulls and digital polyhedra.
The following programs are related to this documentation: geometry/volumes/fullConvexityAnalysis3D.cpp , geometry/volumes/fullConvexityThinning3D.cpp , geometry/volumes/fullConvexityLUT2D.cpp , geometry/volumes/fullConvexityCollapsiblePoints2D.cpp , geometry/volumes/fullConvexityShortestPaths3D.cpp , geometry/volumes/fullConvexitySphereGeodesics.cpp .
Local convexity analysis
Full convexity is stable by intersection with an half-space with axis-aligned normal vector and integer intercept. Hence if \( X \) is fully convex, and \( N_k(x) \) is a \( (2k+1)^d \) neighborhood around point x, then \( X \cap N_k(x) \) is also fully convex.
This shows that a fully convex set is locally fully convex everywhere. Reciprocally local analysis with full convexity gives information on the local geometry:
- \( X \) is k-convex at x, whenever \( X \cap N_k(x) \) is fully convex;
- \( X \) is k-concave at x, whenever \( (\mathbb{Z}^d \setminus X) \cap N_k(x) \) is fully convex;
- \( X \) is k-planar at x, whenever it is both k-convex and k-concave at x;
- otherwise \( X \) is k-atypical at x.
Due to the stability properties of full convexity, one may observe that \( k+1 \)-convexity at x implies \( k \)-convexity at x, the same holds for concavity and planarity. Taking the contraposition indicates that \( k \)-atypicality implies \( k+1 \)-atypicality.
Class NeighborhoodConvexityAnalyzer offers many services to check these properties in an efficient way. It stores look-up tables to perform these services efficiently in 2D for 3x3 neighborhood, and also uses memoization to speed-up computations (useful in dimension greater than 2 and/or when the neighborhood is larger).
The following snippet shows how you can use it.
You may have a look at geometricAnalysis3D.cpp to have a more complete example.

Full convexity analysis at scale 1 | 
Full convexity analysis at scale 2 | 
Full convexity analysis at scale 3 | 
Full convexity analysis at scale 4 |

Full convexity multiscale analysis (scales 1-5) | 
Full convexity smooth multiscale analysis (scales 1-5) |
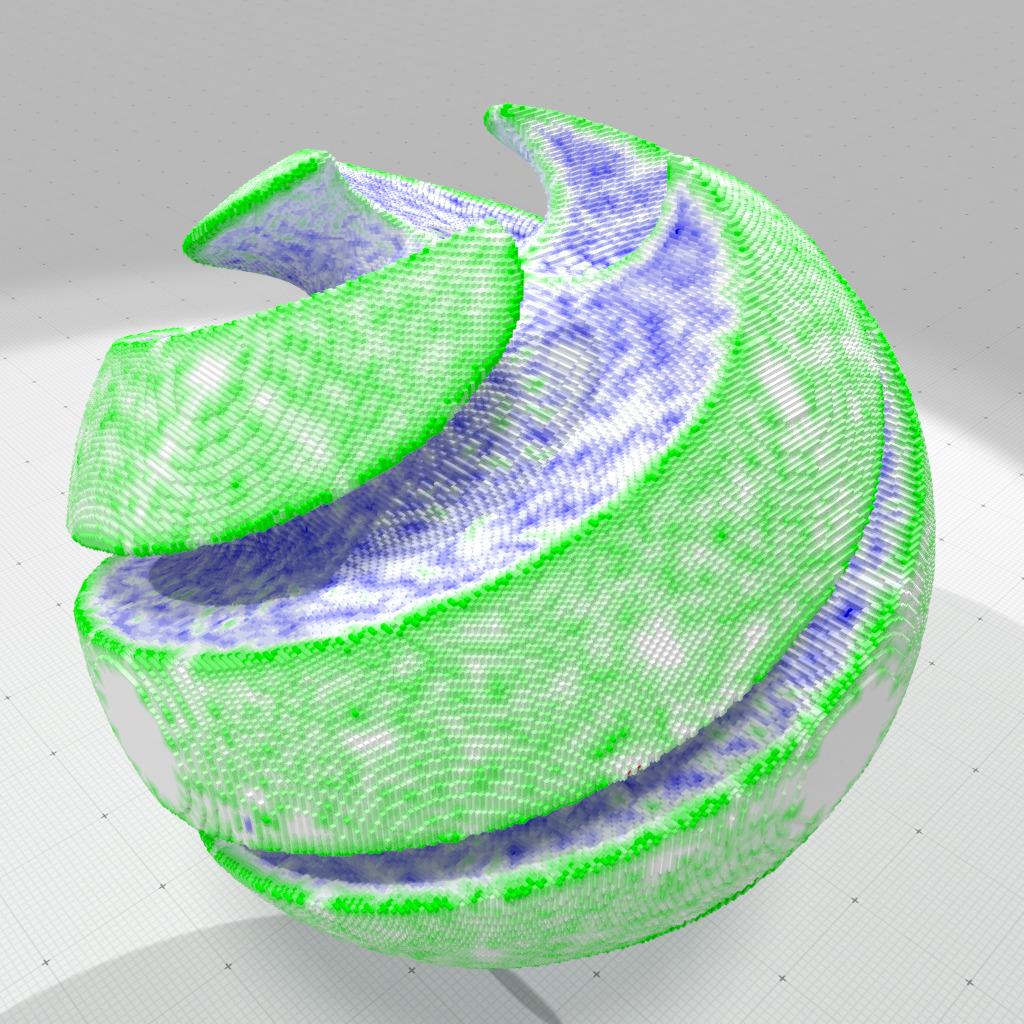
Full convexity smooth multiscale analysis (scales 1-5) | 
Full convexity smooth multiscale analysis (scales 1-5) |
Tangency and shortest paths
Definition of tangency and shortest paths
Tangency or subconvexity is a derived concept from full convexity. Let \( X \subset \mathbb{Z}^d \) some arbitrary digital set. Then the digital set \( A \subset \mathbb{Z}^d \) is said to be digitally k- subconvex to \( X \) whenever \( C^d_k \lbrack \mathrm{Conv}(A) \rbrack \subset C^d_k \lbrack X \rbrack \). And \( A \) is said to be fully (digitally) subconvex to \( X \) whenever it is digitally k- subconvex to \( X \) for \( 0 \le k \le d \).
We also say that \( A \) is tangent to \( X \). The elements of \( A \) are said to be cotangent (in \( X \)). Note that necessarily \( A \subset X \).
A path \( \gamma \) from a to b in \( X \) is then a sequence a points \( \gamma=(x_i)_{i=0,\ldots,n} \), such that \( x_0 = a \), \( x_n = b \), and for all \( i \in \{ 0, \ldots, n-1 \} \), it holds that \( \{ x_i, x_{i+1} \} \) is tangent to \( X \).
We can embed in the Euclidean space the path \( \gamma \) simply by joining its consecutive points by Euclidean straight line segments. Its length is then just the Euclidean length of its embedding.
The cotangency relations define a graph on \( X \), which can be weighted by the length of the Euclidean segments joining cotangent points. Shortest paths on this graph are of course path in the above mentioned sense.
Implementation with TangencyComputer class
The class TangencyComputer offers some services to check tangency and to compute shortest paths:
- TangencyComputer::TangencyComputer requires a cellular grid space big enough to include the future digital object
- TangencyComputer::init defines the points of the digital object
- several accessors are provided to get the space, the points (which are indexed in the same order as initialization), their indices and the cell cover
- TangencyComputer::arePointsCotangent checks if two points are cotangent
- TangencyComputer::getCotangentPoints returns all the indices of the cotangent points to a given point
- TangencyComputer::shortestPath builds the shortest path between a source and a destination
- TangencyComputer::shortestPaths builds all shortest paths to a given source, or builds shortest paths between sources and a set of possible destinations
- TangencyComputer::makeShortestPaths returns a ShortestPaths object, which allows you to compute shortest paths efficiently
To use it, you should include the following headers
Shortest paths to a source
We use here a TangencyComputer::ShortestPaths object to compute and store all shortest paths to a given target point.
The object stores for each point:
- its ancestor in the breadth first traversal (following the sequence of ancestors gives you the shortest path to the target(s))
- its distance to the (closest) target.
Example fullConvexityShortestPaths3D.cpp illustrates that kind of computations, giving the distance of each object point to the specified target.

Geodesic distances and geodesics on cube+sphere shape | 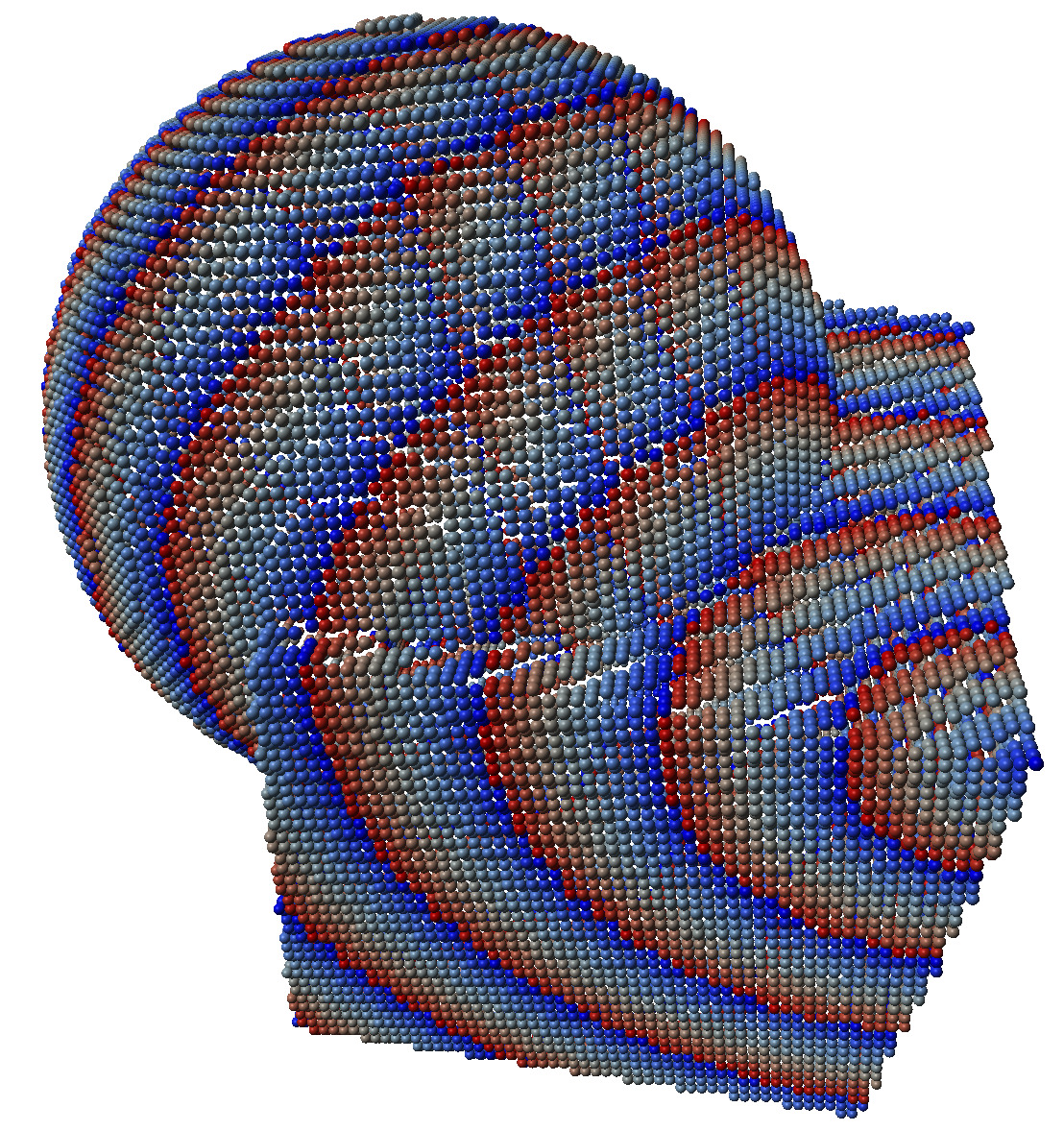
Geodesic distances on cube+sphere shape |
You may obtain nicer views by exporting your result to an OBJ format and then render it.

Geodesic distances on dragon digital surface | 
Geodesic distances on butterfly digital surface |
Shortest path between a source and a target
If you wish to compute only one path, generally it is faster to use breadth first traversal from both the source and the target and stop at first collision. This is already implemented in TangencyComputer::shortestPath, using two TangencyComputer::ShortestPaths objects. The snippet below shows you how it is computed internally:

Approximated shortest paths to speed-up computation
Classes TangencyComputer and TangencyComputer::ShortestPaths offer a way to considerably speed up shortest paths computation if one tolerates a little bit of approximation. Several methods accept a distance parameter K. If K is greater than \( \sqrt{d} \), then shortest paths are exact (meaning all extracted paths are the shortest possible in the sense of the above mentioned algorithm), but if you give a lower value (from \( \sqrt{d} \) to 0 included), you obtain path that may be only shortest path approximations. The table below shows you the trade-off between the speed-up and the approximation error. As one can see, speed-up of \( 50-500 \times \) are obtained, while approximations error are very low or sometimes null.
The following methods accept this parameter:
- TangencyComputer::ShortestPaths::ShortestPaths
- TangencyComputer::makeShortestPaths
- TangencyComputer::shortestPaths
Running the example geometry/volumes/fullConvexitySphereGeodesics.cpp shows the speed-up for different choices of K parameter, as well as the induced approximate distance. In the table below, not surprisingly, the maximum observed distance may be greater in case of approximation. We also indicate if the furthest point to the source point is correct or no.
Table below: Computation times of shortest paths to a given source and maximal error onto a 3D sphere digitized with gridstep \( h \). The chosen \( K \) indicates the chosen distance parameter. Choosing \( K=\|p-q\| \) or \( K=\sqrt{3} \) guarantees the correctness of the output. However, decreasing \( K \) to \( 0 \) speeds up the algorithm, while the maximal relative error in the distance estimation stays very low. Each cell of the last four columns displays the computation time (in seconds), and between parenthesis: OK if the furthest point is the exact antipodal point to the source point on the sphere, and the relative error of the measured shortest path in percentage.
| gridstep h | \( \#(X) \) | Max distance | \( K=\sqrt{3} \) | \( K=\sqrt{3}/4 \) | \( K=\sqrt{3}/16 \) | \( K = 0 \) |
|---|---|---|---|---|---|---|
| 0.25 | 296 | 2.88739 | 0.187 (OK) | 0.068 (OK,0.000%) | 0.024 (OK,0.000%) | 0.013 (OK,0.000%) |
| 0.125 | 1184 | 2.97166 | 1.480 (OK) | 0.470 (OK,0.000%) | 0.177 (OK,0.000%) | 0.082 (OK,0.226%) |
| 0.0625 | 4784 | 3.02389 | 11.744 (OK) | 4.106 (OK,0.000%) | 1.037 (OK,0.000%) | 0.340 (OK,0.538%) |
| 0.03125 | 19256 | 3.08405 | 97.161 (OK) | 39.993 (OK,0.000%) | 9.122 (OK,0.005%) | 2.006 (OK,0.233%) |
| 0.015625 | 77120 | 3.10879 | 1828.890 (OK) | 385.114 (OK,0.000%) | 78.363 (OK,0.038%) | 9.446 (OK,0.289%) |

Exact geodesic distances on unit sphere digitized at h=0.0625 (max d=3.02389) | 
Approximate geodesic distances on unit sphere digitized at h=0.01 (max d=3.1269) |