Table of Contents
- Related DGtalTools:
- shapeGenerator
Introduction of Concepts
In DGtal, we use the generic terminology shape to describe either explicit objects (e.g. spheres, cubes,...) or implicit ones (from a real valued functions, from a predicate on points,...).
An important usage of these notions in DGtal can be found in the shape factory and shape generators tools (see below). However, they can also be used to describe predicate on points (for example to construct a digital set from an image and a binary predicate to describe the region/pixel of interest).
Hence, shapes can be compact or not (i.e. bounded), oriented or not and finally, defined on either the Euclidean space, or the Digital one. All these cases are formalized in the following concepts:
- concepts::CDigitalBoundedShape: Digital shape with lower/upper bounds
- concepts::CEuclideanBoundedShape: Euclidean shape with lower/upper bounds
- concepts::CDigitalOrientedShape: Digital shape with an orientation predicate
- concepts::CEuclideanOrientedShape: Euclidean shape with an orientation predicate
- Note
- An orientation predicate is a method with the following interface: The DGtal::Orientation values can be {INSIDE, ON, OUTSIDE}.Definition testClone2.cpp:346const Point aPoint(3, 4)
Shapers and Digitizers
Given a bounded and oriented shape, we have several process to construct a digital set: given a domain, we can construct the set of points for which the orientation predicate returns INSIDE (defined in Common.h).
For Digital shapes, the set construction (called a shaper in the following) is quite simple since we just have to define the local domain from the shape upper/lower bounds and to scan all grid points.
- Note
- A digital shaper helper method is available in the Shapes class, e.g.: #include <DGtal/shapes/Shapes.h>...Shapes<Domain>::digitalShaper( myOutputSet, myInputShape)
When considering an Euclidean shape \(E\), we first need to specify a digitization process. At this point, DGtal contains a GaussDigitizer parametrized by a step grid h and which construct a digital shape which corresponds to the grid points in \(h\cdot{Z}^n\) which are also in \(E\).
For a flexible digitization, here you have all the steps involved in the digitization of an Euclidean shape (aShape of type Shape):
- Note
- A simpler (but less flexible) possibility is to use the Euclidean shaper helper method is available in the Shapes class, e.g.: In this case, lower and upper bounds are given from the Euclidean shape characteristics.#include <DGtal/shapes/Shapes.h>...Shapes<Domain>::euclideanShaper( myOutputSet, myInputShape, h)
The following figures illustrate the digitization of an ellipse with several grid step values.
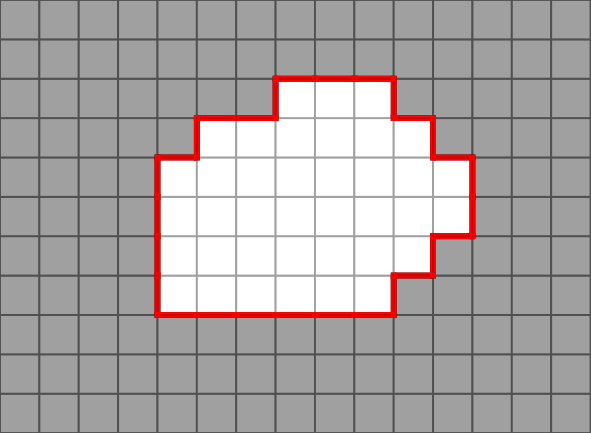


- Note
- A command line tool is available to generate multigrid shapes: shapeGenerator
Shape Factory
DGtal implements many Euclidean shapes to be used in a multigrid analysis of a differential estimator for example. All shapes available in DGtal are models of CEuclideanBoundedShape and CEuclideanOrientedShape.
These shapes are either parametric or implicit ones (see "shapes/parametric" and "shapes/implicit" files). In order to have a simple access to all shapes, just include the "shapes/ShapeFactory.h" header file.
- Note
- In dimension 2, parametric shapes provide fine approximation of differential quantities (length, tangent, curvature,...). These information can be used to evaluate digital differential estimators.
The following pictures illustrate some of the shapes defined in digital in dimension 2 (note that shapes are defined from a set of parameters which are not specified in the captions).


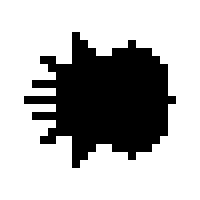

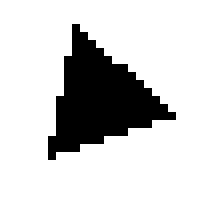



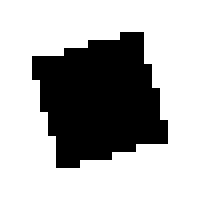

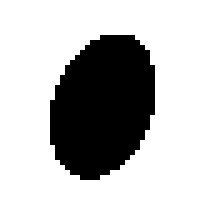
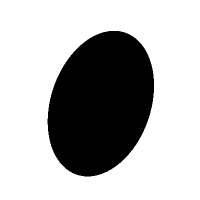



Constructive Solid Geometry tree on Shapes
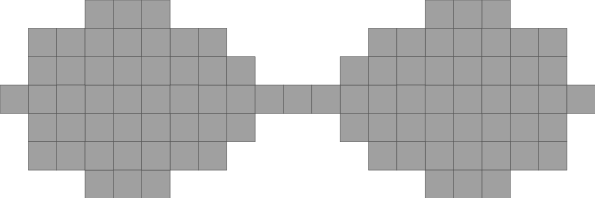
In DGtal, you can also use some CSG operations on Euclidean (resp. Digital) Shapes, using EuclideanShapesCSG (resp. DigitalShapesCSG). See examples in exampleEuclideanShapesDecorator.cpp.
As a root for your CSG tree, you need a shape ShapeA, model of concepts::CEuclideanBoundedShape and concepts::CEuclideanOrientedShape (concepts::CDigitalBoundedShape and concepts::CDigitalOrientedShape). Then, you can add (plus()), remove (minus()), intersect (intersection()) any ShapeB, models of concepts::CEuclideanBoundedShape and concepts::CEuclideanOrientedShape (concepts::CDigitalBoundedShape and concepts::CDigitalOrientedShape) you want. You can combine plus(), minus() and intersection() operations.
Example for minus operation on two Euclidean Shapes :
The following images show you binary operations apply on two Ball2D (results are in orange) and in 3D :



