Table of Contents
- Author(s) of this documentation:
- Pablo Hernandez-Cerdan
- Since
- 0.9.4
Part of the Topology package.
This part of the manual describes how to represent and process arbitrary voxel complexes, which are cubical complexes specialized to work with voxels.
The following programs are related to this documentation: testVoxelComplex.cpp.
Introduction to voxel complexes
This is an implementation of the Critical Kernel framework based on M.Couprie and G.Bertrand articles:
- Asymmetric parallel 3D thinning scheme and algorithms based on isthmuses: https://hal.archives-ouvertes.fr/hal-01217974/document
- Powerful Parallel and Symmetric 3D Thinning Schemes Based on Critical Kernels: https://hal.archives-ouvertes.fr/hal-00828450/
- A 3D Sequential Thinning Scheme Based on Critical Kernels: https://hal.archives-ouvertes.fr/hal-01217952/file/Critical3Dseq.pdf
DGtalTools has an associated command line interface executable: criticalKernelsThinning3D.
Definitions
Summary of definitions used, but highly recommended to read the original manuscripts [39].
- Isthmus:
"Intuitively a voxel x of an object X is said to be a 1-isthmus (resp. a 2-isthmus) if the neighborhood of x corresponds -up to a thinning- to the one of a point belonging to a curve (resp. a surface)."
- Reducible:
We say that the complex X is reducible only if it is possible to reduce it (with thinning) to a single voxel.
- Clique:
Let \( d \in \{0,1,2,3\} \) and let \( C \in V^3 \) with \(V^3\) being the collection of all voxel complexes (a finite set composed solely of voxels). We say that C is a d-clique if the intersection of all voxels of C is a d-face.
Any complex C made of a single voxel is a 3-clique. Furthermore, any voxel of a complex constitutes a 3-clique that is essential for X. Essential is the minimal clique for X.
- K-neighborhood of a voxel S:
Written \(K(S)\) is the set of all voxels adjacent to S. And \(K^*(S) = K \setminus S\).
- Regular clique for the complex X:
We say that the clique C is regular for X if \(K^*(C) \cap X \) is reducible to a single voxel. We say that C is critical for X if C is not regular.
- Note
- If C is a single voxel x, then C is regular for X, only if x is simple for X.
- Theorem:
The complex Y is a thinning of X if any clique that is critical for X, contains at least one voxel of Y.
Critical Kernels:
If we remove simple voxels in parallel is known we may change its topology. Collapse operations used in ParDirCollapse and similar only remove voxels that keep the same topology. Here we use critical kernels to ensure the same homotopy type after thinning.
Initializing a voxel complex.
A voxel complex V is a cubical complex (living in a Khalimsky space).
To create a VoxelComplex, we need to specify in which Khalimsky space it lives and also, optionally, the type of container used for storing cells.
Last, there is a data associated with each cell of a complex. The data type must either be CubicalCellData or a type that derives from CubicalCellData. This data is used by the thinning algorithm with persistence. But can be used for other purposes, take a look at the documentation of CubicalCellData to see the default stored flags and data.
Implementation Details
The details of the implementation can be summarized int he implementation of four masks that given a d-cell (pointel, linel, surfel, spel) returns a d-clique and a boolean flag with its criticality.
VoxelComplex::K_0,VoxelComplex::K_1, VoxelComplex::K_2, and VoxelComplex::K_3 return a pair<bool, Clique> where Clique=CubicalComplex, and the bool is true if the Clique is critical.
VoxelComplex::K_3 applies to Voxels, it can either create a small object to use the isSimple method of Object, or if a pre-compute LUT table of simplicity is loaded, it will look up the result based on the occupancy of the neighborhood (recommended).
VoxelComplex::K_2 applies to surfels,
VoxelComplex::K_1 to linels, and VoxelComplex::K_0 to pointels.
Thinning in voxel complexes
In VoxelComplexFunctions.h a couple of thinning methods are implemented in a functional style, taking a VoxelComplex, a Select function, and a Skel function.
functions::asymetricThinningScheme and functions::persistenceAsymetricThinningScheme. These algorithms are homeotopic, keeping the topology of the original object.
The only difference between both algorithms is the persistence parameter, which allow to perform trimming on spurious or branches generated by noise.
Select function: Select a voxel from a clique (set of voxels)
- functions::selectRandom.
- functions::selectFirst: just the first voxel of the set ordered in a lexicographical order.
- functions::selectMaxValue: Wrap to use with a lambda, to use a DistanceTransformation to select the voxel with greatest distance value.
Skel function: Predicate to check if input voxel is part of the skeleton that we are interested to preserve.
- functions::skelUltimate: Null, preserve only to keep same topology. The result of the thinning in a connected object without holes is just one voxel.
- functions::skelEnd: preserve if voxel has only one neighbor.
- OneIsthmus: preserve if voxel is oneIsthmus, as described in articles. Prefer to use the 1isthmus LUT for speed.
- TwoIsthmus: idem, this conserves planar structures.
- skelIsthmus : (OneIsthmus || TwoIsthmus). Prefer to use the isthmus LUT for speed.
- functions::skelWithTable: Wrap to use with a lambda, that accept any table from LookUpTable. Right now we provide tables for 26_6 topology for isthmus and one-isthmus. Generated using: functions::generateVoxelComplexTable.
testVoxelComplex.cpp provides example of how to use with isIsthmus table.
The only difference between both algorithms is the persistence parameter, which allow to perform trimming on spurious or branches generated by noise.


The persistence parameter controls the removal of voxels from the skeleton (voxels where the Skel function returns true). Every generation in the algorithm runs over every voxel, checking if they can be removed (because they don't change the topology) and if they have to be kept because they are part of the skeleton.
So every voxel, through the associated CellData of VoxelComplex store the value of the first generation they became an isthmus (or any other Skel function), as a birth date. Then, they are finally kept into the constraint K set if they are still an isthmus and they are persistent enough.
Examples
DGtalTools provide a script criticalKernelsThinning3D.cpp ready to use for 3D inputs. Some results:

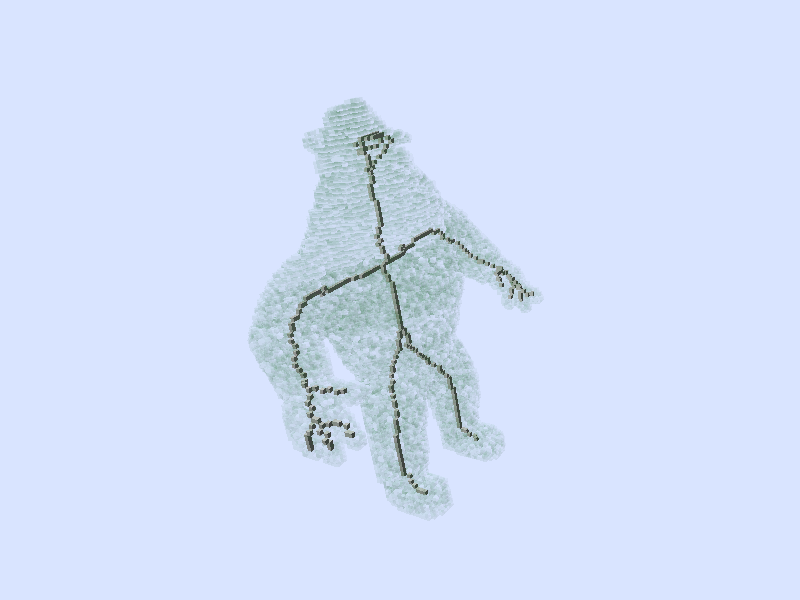

When the input set has noise in the borders, the persistence automatic trimming is pretty useful.