geometry/volumes/pConvexity-benchmark.cpp
This example compares the speed of computation of P-convexity wrt to the computation of full convexity. Both definitions are equivalent but P-convexity is faster to compute, especially in higher dimensions.
pConvexity-benchmark
Simply run the benchmark (it will take more than 1 hour on a M2 pro chip). It produces 9 files "timings-p-convexity-Z[d].txt", "timings-fc-convexity-Z[d].txt", and "timings-fcf-convexity-Z[d].txt", corresponding to P-convexity/full convexity/fast full convexity computation in Z[d]. Each data is a triplet (number of points, timings in ms, isConvex).
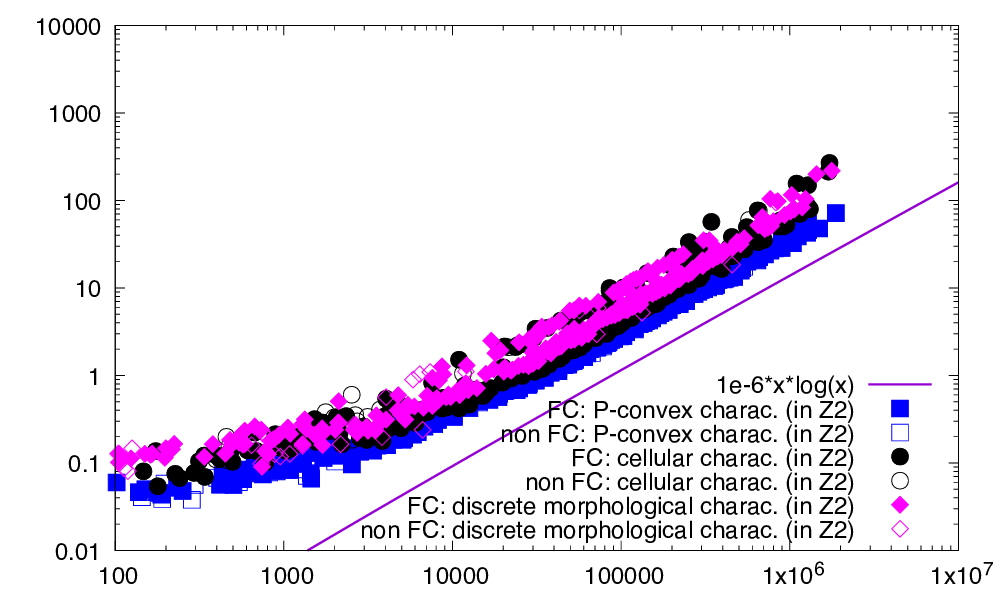
Computation times (ms) of P-convexity wrt full convexity in Z2 as a function of the cardinal of the digital set. P-convexity is generally 2-3x faster to compute.
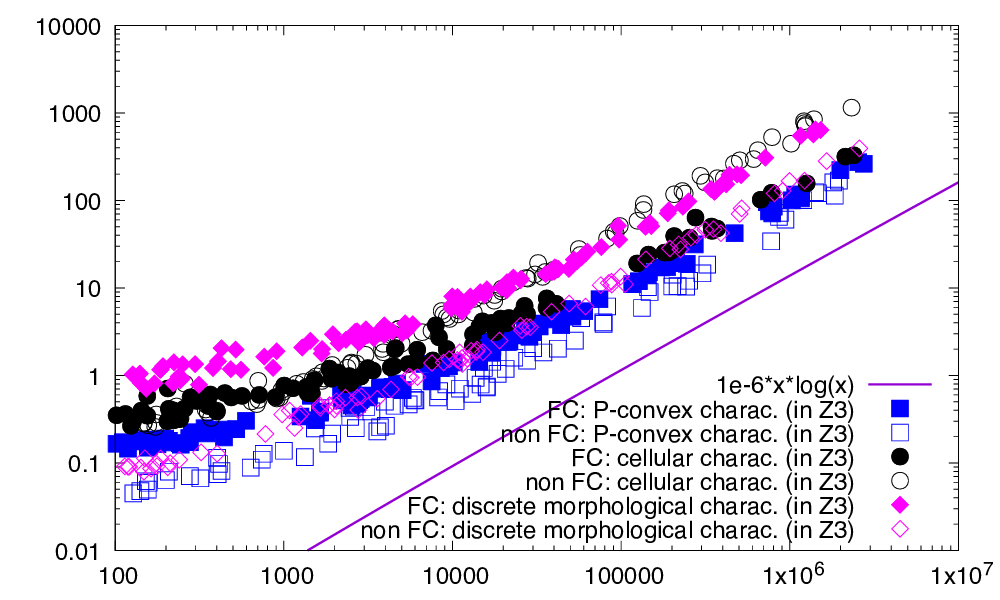
Computation times (ms) of P-convexity wrt full convexity in Z3 as a function of the cardinal of the digital set. P-convexity is generally 3-10x faster to compute. The difference is greater for non P-convex / non fully convex sets.
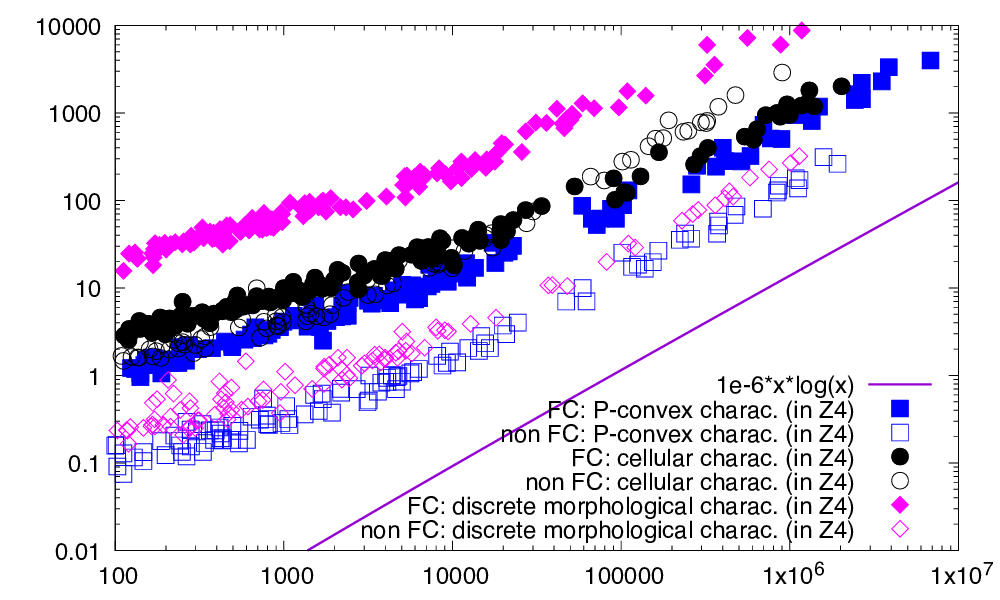
Computation times (ms) of P-convexity wrt full convexity in Z4 as a function of the cardinal of the digital set. P-convexity is generally 3-20x faster to compute. The difference is greater for non P-convex / non fully convex sets.
#include <iostream>
#include <vector>
#include <algorithm>
#include <chrono>
#include "DGtal/base/Common.h"
#include "DGtal/kernel/SpaceND.h"
#include "DGtal/kernel/domains/HyperRectDomain.h"
#include "DGtal/kernel/sets/DigitalSetBySTLSet.h"
#include "DGtal/topology/KhalimskySpaceND.h"
#include "DGtal/shapes/Shapes.h"
#include "DGtal/geometry/volumes/PConvexity.h"
#include "DGtal/geometry/volumes/DigitalConvexity.h"
using namespace std;
using namespace DGtal;
template <Dimension dim>
void
timingsPConvexity( std::vector< std::tuple< std::size_t, double, bool > >& results,
std::size_t nb_tries, std::size_t nb_vertices, std::size_t range,
double pconvexity_probability = 0.5 )
{
typedef PConvexity< Space > PConvexity;
DConvexity dconv( Point::diagonal( -1 ), Point::diagonal( range ) );
PConvexity pconv;
for ( auto n = 0; n < nb_tries; ++n )
{
// Create vertices
std::vector< Point > V;
for ( auto i = 0; i < nb_vertices; i++ ) {
Point p;
V.push_back( p );
}
// create 0-convex or fully convex set.
std::vector< Point > X;
bool force_pconvexity = rand01() < pconvexity_probability;
if ( force_pconvexity )
X = dconv.envelope( V );
else
{
P.getPoints( X );
}
// Analyse P-convexity
std::chrono::high_resolution_clock::time_point
t1 = std::chrono::high_resolution_clock::now();
bool is_pconvex = pconv.isPConvex( X );
std::chrono::high_resolution_clock::time_point
t2 = std::chrono::high_resolution_clock::now();
results.push_back( std::make_tuple( X.size(), dt/1e6, is_pconvex ) );
if ( force_pconvexity && ! is_pconvex )
}
}
template <Dimension dim>
void
timingsFullConvexity( std::vector< std::tuple< std::size_t, double, bool > >& results,
std::size_t nb_tries, std::size_t nb_vertices, std::size_t range,
double fconvexity_probability = 0.5 )
{
typedef KhalimskySpaceND<dim,int64_t> KSpace;
typedef DigitalConvexity< KSpace > DConvexity;
typedef PConvexity< Space > PConvexity;
DConvexity dconv( Point::diagonal( -1 ), Point::diagonal( range ) );
PConvexity pconv;
for ( auto n = 0; n < nb_tries; ++n )
{
// Create vertices
std::vector< Point > V;
for ( auto i = 0; i < nb_vertices; i++ ) {
Point p;
V.push_back( p );
}
// create 0-convex or fully convex set.
std::vector< Point > X;
bool force_fconvexity = rand01() < fconvexity_probability;
if ( force_fconvexity )
X = dconv.envelope( V );
else
{
auto P = dconv.CvxH( V );
P.getPoints( X );
}
// Analyse full convexity
std::chrono::high_resolution_clock::time_point
t1 = std::chrono::high_resolution_clock::now();
std::chrono::high_resolution_clock::time_point
t2 = std::chrono::high_resolution_clock::now();
double dt = std::chrono::duration_cast<std::chrono::nanoseconds>(t2 - t1).count();
results.push_back( std::make_tuple( X.size(), dt/1e6, is_fconvex ) );
if ( force_fconvexity && ! is_fconvex )
}
}
template <Dimension dim>
void
timingsFullConvexityFast( std::vector< std::tuple< std::size_t, double, bool > >& results,
std::size_t nb_tries, std::size_t nb_vertices, std::size_t range,
double fconvexity_probability = 0.5 )
{
typedef KhalimskySpaceND<dim,int64_t> KSpace;
typedef DigitalConvexity< KSpace > DConvexity;
typedef PConvexity< Space > PConvexity;
DConvexity dconv( Point::diagonal( -1 ), Point::diagonal( range ) );
PConvexity pconv;
for ( auto n = 0; n < nb_tries; ++n )
{
// Create vertices
std::vector< Point > V;
for ( auto i = 0; i < nb_vertices; i++ ) {
Point p;
V.push_back( p );
}
// create 0-convex or fully convex set.
std::vector< Point > X;
bool force_fconvexity = rand01() < fconvexity_probability;
if ( force_fconvexity )
X = dconv.envelope( V );
else
{
auto P = dconv.CvxH( V );
P.getPoints( X );
}
// Analyse full convexity
std::chrono::high_resolution_clock::time_point
t1 = std::chrono::high_resolution_clock::now();
std::chrono::high_resolution_clock::time_point
t2 = std::chrono::high_resolution_clock::now();
double dt = std::chrono::duration_cast<std::chrono::nanoseconds>(t2 - t1).count();
results.push_back( std::make_tuple( X.size(), dt/1e6, is_fconvex ) );
if ( force_fconvexity && ! is_fconvex )
}
}
template <Dimension dim>
void
( std::vector< std::tuple< std::size_t, double, bool > >& results,
std::size_t nb_tries, std::size_t range )
{
typedef KhalimskySpaceND<dim,int64_t> KSpace;
typedef DigitalConvexity< KSpace > DConvexity;
typedef PConvexity< Space > PConvexity;
DConvexity dconv( Point::diagonal( -1 ), Point::diagonal( range ) );
PConvexity pconv;
for ( auto n = 0; n < nb_tries; ++n )
{
double filling_probability = 0.1 + 0.9 * double( n ) / double( nb_tries );
// Create vertices
std::set< Point > S;
std::size_t nb_vertices
= std::size_t( filling_probability * ceil( pow( range, dim ) ) );
for ( auto i = 0; i < nb_vertices; i++ ) {
Point p;
S.insert( p );
}
// create digital set.
std::vector< Point > X( S.cbegin(), S.cend() );
// Analyse P-convexity
std::chrono::high_resolution_clock::time_point
t1 = std::chrono::high_resolution_clock::now();
bool is_pconvex = pconv.isPConvex( X );
std::chrono::high_resolution_clock::time_point
t2 = std::chrono::high_resolution_clock::now();
double dt = std::chrono::duration_cast<std::chrono::nanoseconds>(t2 - t1).count();
results.push_back( std::make_tuple( X.size(), dt/1e6, is_pconvex ) );
}
}
template <Dimension dim>
void
( std::vector< std::tuple< std::size_t, double, bool > >& results,
std::size_t nb_tries, std::size_t range )
{
typedef KhalimskySpaceND<dim,int64_t> KSpace;
typedef DigitalConvexity< KSpace > DConvexity;
typedef PConvexity< Space > PConvexity;
DConvexity dconv( Point::diagonal( -1 ), Point::diagonal( range ) );
PConvexity pconv;
for ( auto n = 0; n < nb_tries; ++n )
{
double filling_probability = 0.1 + 0.9 * double( n ) / double( nb_tries );
// Create vertices
std::set< Point > S;
std::size_t nb_vertices
= std::size_t( filling_probability * ceil( pow( range, dim ) ) );
for ( auto i = 0; i < nb_vertices; i++ ) {
Point p;
S.insert( p );
}
// create digital set.
std::vector< Point > X( S.cbegin(), S.cend() );
// Analyse full convexity
std::chrono::high_resolution_clock::time_point
t1 = std::chrono::high_resolution_clock::now();
bool is_fconvex = dconv.isFullyConvex( X );
std::chrono::high_resolution_clock::time_point
t2 = std::chrono::high_resolution_clock::now();
double dt = std::chrono::duration_cast<std::chrono::nanoseconds>(t2 - t1).count();
results.push_back( std::make_tuple( X.size(), dt/1e6, is_fconvex ) );
}
}
template <Dimension dim>
void
( std::vector< std::tuple< std::size_t, double, bool > >& results,
std::size_t nb_tries, std::size_t range )
{
typedef KhalimskySpaceND<dim,int64_t> KSpace;
typedef DigitalConvexity< KSpace > DConvexity;
typedef PConvexity< Space > PConvexity;
DConvexity dconv( Point::diagonal( -1 ), Point::diagonal( range ) );
PConvexity pconv;
for ( auto n = 0; n < nb_tries; ++n )
{
double filling_probability = 0.1 + 0.9 * double( n ) / double( nb_tries );
// Create vertices
std::set< Point > S;
std::size_t nb_vertices
= std::size_t( filling_probability * ceil( pow( range, dim ) ) );
for ( auto i = 0; i < nb_vertices; i++ ) {
Point p;
S.insert( p );
}
// create digital set.
std::vector< Point > X( S.cbegin(), S.cend() );
// Analyse full convexity
std::chrono::high_resolution_clock::time_point
t1 = std::chrono::high_resolution_clock::now();
bool is_fconvex = dconv.isFullyConvexFast( X );
std::chrono::high_resolution_clock::time_point
t2 = std::chrono::high_resolution_clock::now();
double dt = std::chrono::duration_cast<std::chrono::nanoseconds>(t2 - t1).count();
results.push_back( std::make_tuple( X.size(), dt/1e6, is_fconvex ) );
}
}
const std::vector< std::tuple< std::size_t, double, bool > >& results,
const std::string& fname )
{
std::ofstream output( fname );
output << "# Results of " << results.size() << " P-convexity computations in Z"
<< dim << std::endl
<< "# Card(X) time(ms) p-convex?" << std::endl;
for ( auto&& r : results )
output << std::get<0>( r ) << " " << std::get<1>( r ) << " " << std::get<2>( r )
<< std::endl;
output.close();
}
/*
Display results using gnuplot
plot "./timings-p-convexity-Z2.txt" using 1:2 w p, "./timings-p-convexity-Z3.txt" using 1:2 w p,"./timings-p-convexity-Z4.txt" using 1:2 w p, 0.2e-5*x*log(x) w l lw 2
plot "./timings-p-convexity-Z2.txt" using 1:($3 == 1 ? $2 : 1/0) title "P-convex in Z2" w p, "./timings-p-convexity-Z2.txt" using 1:($3 == 0 ? $2 : 1/0) title "non P-convex in Z2" w p, 0.2e-5*x*log(x) w l lw 2
plot "./timings-p-convexity-Z3.txt" using 1:($3 == 1 ? $2 : 1/0) title "P-convex in Z3" w p, "./timings-p-convexity-Z3.txt" using 1:($3 == 0 ? $2 : 1/0) title "non P-convex in Z3" w p, 0.4e-5*x*log(x) w l lw 2
plot "./timings-p-convexity-Z4.txt" using 1:($3 == 1 ? $2 : 1/0) title "P-convex in Z4" w p, "./timings-p-convexity-Z4.txt" using 1:($3 == 0 ? $2 : 1/0) title "non P-convex in Z4" w p, 0.4e-5*x*log(x) w l lw 2
set terminal eps font "Helvetica,14"
set key bottom right
plot [1e2:1e7][1e-2:1e4] 1e-6*x*log(x) w l lw 3, "./timings-p-convexity-Z2.txt" using 1:($3 == 1 ? $2 : 1/0) title "FC: P-convex charac. (in Z2)" w p pt 5 lc rgb "blue", "./timings-p-convexity-Z2.txt" using 1:($3 == 0 ? $2 : 1/0) title "non FC: P-convex charac. (in Z2)" w p pt 4 lc rgb "blue", "./timings-fcf-convexity-Z2.txt" using 1:($3 == 1 ? $2 : 1/0) title "FC: cellular charac. (in Z2)" w p pt 7 lc rgb "black", "./timings-fcf-convexity-Z2.txt" using 1:($3 == 0 ? $2 : 1/0) title "non FC: cellular charac. (in Z2)" w p pt 6 lc rgb "black", "./timings-fc-convexity-Z2.txt" using 1:($3 == 1 ? $2 : 1/0) title "FC: discrete morphological charac. (in Z2)" w p pt 13 lc rgb "magenta", "./timings-fc-convexity-Z2.txt" using 1:($3 == 0 ? $2 : 1/0) title "non FC: discrete morphological charac. (in Z2)" w p pt 12 lc rgb "magenta"
plot [1e2:1e7][1e-2:1e4] 1e-6*x*log(x) w l lw 3, "./timings-p-convexity-Z3.txt" using 1:($3 == 1 ? $2 : 1/0) title "FC: P-convex charac. (in Z3)" w p pt 5 lc rgb "blue", "./timings-p-convexity-Z3.txt" using 1:($3 == 0 ? $2 : 1/0) title "non FC: P-convex charac. (in Z3)" w p pt 4 lc rgb "blue", "./timings-fcf-convexity-Z3.txt" using 1:($3 == 1 ? $2 : 1/0) title "FC: cellular charac. (in Z3)" w p pt 7 lc rgb "black", "./timings-fcf-convexity-Z3.txt" using 1:($3 == 0 ? $2 : 1/0) title "non FC: cellular charac. (in Z3)" w p pt 6 lc rgb "black", "./timings-fc-convexity-Z3.txt" using 1:($3 == 1 ? $2 : 1/0) title "FC: discrete morphological charac. (in Z3)" w p pt 13 lc rgb "magenta", "./timings-fc-convexity-Z3.txt" using 1:($3 == 0 ? $2 : 1/0) title "non FC: discrete morphological charac. (in Z3)" w p pt 12 lc rgb "magenta"
plot [1e2:1e7][1e-2:1e4] 1e-6*x*log(x) w l lw 3, "./timings-p-convexity-Z4.txt" using 1:($3 == 1 ? $2 : 1/0) title "FC: P-convex charac. (in Z4)" w p pt 5 lc rgb "blue", "./timings-p-convexity-Z4.txt" using 1:($3 == 0 ? $2 : 1/0) title "non FC: P-convex charac. (in Z4)" w p pt 4 lc rgb "blue", "./timings-fcf-convexity-Z4.txt" using 1:($3 == 1 ? $2 : 1/0) title "FC: cellular charac. (in Z4)" w p pt 7 lc rgb "black", "./timings-fcf-convexity-Z4.txt" using 1:($3 == 0 ? $2 : 1/0) title "non FC: cellular charac. (in Z4)" w p pt 6 lc rgb "black", "./timings-fc-convexity-Z4.txt" using 1:($3 == 1 ? $2 : 1/0) title "FC: discrete morphological charac. (in Z4)" w p pt 13 lc rgb "magenta", "./timings-fc-convexity-Z4.txt" using 1:($3 == 0 ? $2 : 1/0) title "non FC: discrete morphological charac. (in Z4)" w p pt 12 lc rgb "magenta"
set terminal eps font "Helvetica,12"
set key bottom right
plot [1e2:1e7][1e-2:1e4] 1e-6*x*log(x) w l lw 3, "./timings-p-convexity-ncvx-Z2.txt" using 1:2 title "P-convex charac. (in Z2)" w p pt 4 lc rgb "blue", "./timings-fc-convexity-ncvx-Z2.txt" using 1:2 title "discrete morphological charac. (in Z2)" w p pt 12 lc rgb "magenta", "./timings-fcf-convexity-ncvx-Z2.txt" using 1:2 title "cellular charac. (in Z2)" w p pt 6 lc rgb "black"
plot [1e2:1e7][1e-2:1e4] 1e-6*x*log(x) w l lw 3, "./timings-p-convexity-ncvx-Z3.txt" using 1:2 title "P-convex charac. (in Z3)" w p pt 4 lc rgb "blue", "./timings-fc-convexity-ncvx-Z3.txt" using 1:2 title "discrete morphological charac. (in Z3)" w p pt 12 lc rgb "magenta", "./timings-fcf-convexity-ncvx-Z3.txt" using 1:2 title "cellular charac. (in Z3)" w p pt 6 lc rgb "black"
plot [1e2:1e7][1e-2:1e4] 1e-6*x*log(x) w l lw 3, "./timings-p-convexity-ncvx-Z4.txt" using 1:2 title "P-convex charac. (in Z4)" w p pt 4 lc rgb "blue", "./timings-fc-convexity-ncvx-Z4.txt" using 1:2 title "discrete morphological charac. (in Z4)" w p pt 12 lc rgb "magenta", "./timings-fcf-convexity-ncvx-Z4.txt" using 1:2 title "cellular charac. (in Z4)" w p pt 6 lc rgb "black"
*/
{
// P-convexity
srand( 0 );
if ( false )
{
std::vector< std::tuple< std::size_t, double, bool > > R2;
timingsPConvexity<2>( R2, 50, 3, 100, 0.5 );
timingsPConvexity<2>( R2, 50, 4, 200, 0.5 );
timingsPConvexity<2>( R2, 50, 5, 400, 0.5 );
timingsPConvexity<2>( R2, 50, 5, 600, 0.5 );
timingsPConvexity<2>( R2, 50, 5, 800, 0.5 );
timingsPConvexity<2>( R2, 25, 5,1200, 0.5 );
timingsPConvexity<2>( R2, 25, 5,2000, 0.5 );
outputResults( 2, R2, "timings-p-convexity-Z2.txt" );
}
if ( false )
{
std::vector< std::tuple< std::size_t, double, bool > > R3;
timingsPConvexity<3>( R3, 50, 3, 10, 0.5 );
timingsPConvexity<3>( R3, 50, 4, 20, 0.5 );
timingsPConvexity<3>( R3, 50, 5, 40, 0.5 );
timingsPConvexity<3>( R3, 50, 5, 80, 0.5 );
timingsPConvexity<3>( R3, 25, 5, 160, 0.5 );
timingsPConvexity<3>( R3, 25, 5, 320, 0.5 );
outputResults( 3, R3, "timings-p-convexity-Z3.txt" );
}
if ( false )
{
std::vector< std::tuple< std::size_t, double, bool > > R4;
timingsPConvexity<4>( R4, 50, 5, 10, 0.5 );
timingsPConvexity<4>( R4, 50, 5, 15, 0.5 );
timingsPConvexity<4>( R4, 50, 5, 20, 0.5 );
timingsPConvexity<4>( R4, 50, 5, 30, 0.5 );
timingsPConvexity<4>( R4, 25, 5, 40, 0.5 );
timingsPConvexity<4>( R4, 25, 5, 60, 0.5 );
timingsPConvexity<4>( R4, 15, 6, 80, 0.5 );
timingsPConvexity<4>( R4, 15, 6, 100, 0.5 );
timingsPConvexity<4>( R4, 15, 6, 120, 0.5 );
outputResults( 4, R4, "timings-p-convexity-Z4.txt" );
}
// Full convexity
srand( 0 );
if ( false )
{
std::vector< std::tuple< std::size_t, double, bool > > R2;
timingsFullConvexity<2>( R2, 50, 3, 100, 0.5 );
timingsFullConvexity<2>( R2, 50, 4, 200, 0.5 );
timingsFullConvexity<2>( R2, 50, 5, 400, 0.5 );
timingsFullConvexity<2>( R2, 50, 5, 600, 0.5 );
timingsFullConvexity<2>( R2, 50, 5, 800, 0.5 );
timingsFullConvexity<2>( R2, 25, 5,1200, 0.5 );
timingsFullConvexity<2>( R2, 25, 5,2000, 0.5 );
outputResults( 2, R2, "timings-fc-convexity-Z2.txt" );
}
if ( false )
{
std::vector< std::tuple< std::size_t, double, bool > > R3;
timingsFullConvexity<3>( R3, 50, 3, 10, 0.5 );
timingsFullConvexity<3>( R3, 50, 4, 20, 0.5 );
timingsFullConvexity<3>( R3, 50, 5, 40, 0.5 );
timingsFullConvexity<3>( R3, 50, 5, 80, 0.5 );
timingsFullConvexity<3>( R3, 25, 5, 160, 0.5 );
timingsFullConvexity<3>( R3, 25, 5, 320, 0.5 );
outputResults( 3, R3, "timings-fc-convexity-Z3.txt" );
}
if ( false )
{
std::vector< std::tuple< std::size_t, double, bool > > R4;
timingsFullConvexity<4>( R4, 50, 5, 10, 0.5 );
timingsFullConvexity<4>( R4, 50, 5, 15, 0.5 );
timingsFullConvexity<4>( R4, 50, 5, 20, 0.5 );
timingsFullConvexity<4>( R4, 50, 5, 30, 0.5 );
timingsFullConvexity<4>( R4, 25, 5, 40, 0.5 );
timingsFullConvexity<4>( R4, 25, 5, 60, 0.5 );
timingsFullConvexity<4>( R4, 15, 6, 80, 0.5 );
timingsFullConvexity<4>( R4, 10, 6, 100, 0.5 );
timingsFullConvexity<4>( R4, 5, 6, 120, 0.5 );
outputResults( 4, R4, "timings-fc-convexity-Z4.txt" );
}
// Full convexity fast
srand( 0 );
if ( false )
{
std::vector< std::tuple< std::size_t, double, bool > > R2;
timingsFullConvexityFast<2>( R2, 50, 3, 100, 0.5 );
timingsFullConvexityFast<2>( R2, 50, 4, 200, 0.5 );
timingsFullConvexityFast<2>( R2, 50, 5, 400, 0.5 );
timingsFullConvexityFast<2>( R2, 50, 5, 600, 0.5 );
timingsFullConvexityFast<2>( R2, 50, 5, 800, 0.5 );
timingsFullConvexityFast<2>( R2, 25, 5,1200, 0.5 );
timingsFullConvexityFast<2>( R2, 25, 5,2000, 0.5 );
outputResults( 2, R2, "timings-fcf-convexity-Z2.txt" );
}
if ( false )
{
std::vector< std::tuple< std::size_t, double, bool > > R3;
timingsFullConvexityFast<3>( R3, 50, 3, 10, 0.5 );
timingsFullConvexityFast<3>( R3, 50, 4, 20, 0.5 );
timingsFullConvexityFast<3>( R3, 50, 5, 40, 0.5 );
timingsFullConvexityFast<3>( R3, 50, 5, 80, 0.5 );
timingsFullConvexityFast<3>( R3, 25, 5, 160, 0.5 );
timingsFullConvexityFast<3>( R3, 25, 5, 320, 0.5 );
outputResults( 3, R3, "timings-fcf-convexity-Z3.txt" );
}
if ( false )
{
std::vector< std::tuple< std::size_t, double, bool > > R4;
timingsFullConvexityFast<4>( R4, 50, 5, 10, 0.5 );
timingsFullConvexityFast<4>( R4, 50, 5, 15, 0.5 );
timingsFullConvexityFast<4>( R4, 50, 5, 20, 0.5 );
timingsFullConvexityFast<4>( R4, 50, 5, 30, 0.5 );
timingsFullConvexityFast<4>( R4, 25, 5, 40, 0.5 );
timingsFullConvexityFast<4>( R4, 25, 5, 60, 0.5 );
timingsFullConvexityFast<4>( R4, 15, 6, 80, 0.5 );
timingsFullConvexityFast<4>( R4, 10, 6, 100, 0.5 );
timingsFullConvexityFast<4>( R4, 5, 6, 120, 0.5 );
outputResults( 4, R4, "timings-fcf-convexity-Z4.txt" );
}
// P-convexity
srand( 0 );
if ( false )
{
std::vector< std::tuple< std::size_t, double, bool > > R2;
timingsPConvexityNonConvex<2>( R2, 50, 100 );
timingsPConvexityNonConvex<2>( R2, 50, 200 );
timingsPConvexityNonConvex<2>( R2, 50, 400 );
timingsPConvexityNonConvex<2>( R2, 50, 600 );
timingsPConvexityNonConvex<2>( R2, 50, 800 );
timingsPConvexityNonConvex<2>( R2, 50, 1200 );
timingsPConvexityNonConvex<2>( R2, 50, 2000 );
outputResults( 2, R2, "timings-p-convexity-ncvx-Z2.txt" );
}
if ( false )
{
std::vector< std::tuple< std::size_t, double, bool > > R3;
timingsPConvexityNonConvex<3>( R3, 50, 20 );
timingsPConvexityNonConvex<3>( R3, 50, 40 );
timingsPConvexityNonConvex<3>( R3, 50, 80 );
timingsPConvexityNonConvex<3>( R3, 50, 160 );
timingsPConvexityNonConvex<3>( R3, 50, 320 );
outputResults( 3, R3, "timings-p-convexity-ncvx-Z3.txt" );
}
if ( false )
{
std::vector< std::tuple< std::size_t, double, bool > > R4;
timingsPConvexityNonConvex<4>( R4, 50, 10 );
timingsPConvexityNonConvex<4>( R4, 50, 20 );
timingsPConvexityNonConvex<4>( R4, 50, 30 );
timingsPConvexityNonConvex<4>( R4, 40, 40 );
timingsPConvexityNonConvex<4>( R4, 20, 50 );
outputResults( 4, R4, "timings-p-convexity-ncvx-Z4.txt" );
}
if ( false )
{
std::vector< std::tuple< std::size_t, double, bool > > R2;
timingsFullConvexityNonConvex<2>( R2, 50, 100 );
timingsFullConvexityNonConvex<2>( R2, 50, 200 );
timingsFullConvexityNonConvex<2>( R2, 50, 400 );
timingsFullConvexityNonConvex<2>( R2, 50, 600 );
timingsFullConvexityNonConvex<2>( R2, 50, 800 );
timingsFullConvexityNonConvex<2>( R2, 50, 1200 );
timingsFullConvexityNonConvex<2>( R2, 50, 2000 );
outputResults( 2, R2, "timings-fc-convexity-ncvx-Z2.txt" );
}
if ( false )
{
std::vector< std::tuple< std::size_t, double, bool > > R3;
timingsFullConvexityNonConvex<3>( R3, 50, 20 );
timingsFullConvexityNonConvex<3>( R3, 50, 40 );
timingsFullConvexityNonConvex<3>( R3, 50, 80 );
timingsFullConvexityNonConvex<3>( R3, 40, 160 );
timingsFullConvexityNonConvex<3>( R3, 25, 320 );
outputResults( 3, R3, "timings-fc-convexity-ncvx-Z3.txt" );
}
if ( false )
{
std::vector< std::tuple< std::size_t, double, bool > > R4;
timingsFullConvexityNonConvex<4>( R4, 50, 10 );
timingsFullConvexityNonConvex<4>( R4, 50, 20 );
timingsFullConvexityNonConvex<4>( R4, 50, 30 );
timingsFullConvexityNonConvex<4>( R4, 40, 40 );
timingsFullConvexityNonConvex<4>( R4, 20, 50 );
outputResults( 4, R4, "timings-fc-convexity-ncvx-Z4.txt" );
}
if ( false )
{
std::vector< std::tuple< std::size_t, double, bool > > R2;
timingsFullConvexityFastNonConvex<2>( R2, 50, 100 );
timingsFullConvexityFastNonConvex<2>( R2, 50, 200 );
timingsFullConvexityFastNonConvex<2>( R2, 50, 400 );
timingsFullConvexityFastNonConvex<2>( R2, 50, 600 );
timingsFullConvexityFastNonConvex<2>( R2, 50, 800 );
timingsFullConvexityFastNonConvex<2>( R2, 50, 1200 );
timingsFullConvexityFastNonConvex<2>( R2, 50, 2000 );
outputResults( 2, R2, "timings-fcf-convexity-ncvx-Z2.txt" );
}
if ( false )
{
std::vector< std::tuple< std::size_t, double, bool > > R3;
timingsFullConvexityFastNonConvex<3>( R3, 50, 20 );
timingsFullConvexityFastNonConvex<3>( R3, 50, 40 );
timingsFullConvexityFastNonConvex<3>( R3, 50, 80 );
timingsFullConvexityFastNonConvex<3>( R3, 40, 160 );
timingsFullConvexityFastNonConvex<3>( R3, 25, 320 );
outputResults( 3, R3, "timings-fcf-convexity-ncvx-Z3.txt" );
}
if ( false )
{
std::vector< std::tuple< std::size_t, double, bool > > R4;
timingsFullConvexityFastNonConvex<4>( R4, 50, 10 );
timingsFullConvexityFastNonConvex<4>( R4, 50, 20 );
timingsFullConvexityFastNonConvex<4>( R4, 50, 30 );
timingsFullConvexityFastNonConvex<4>( R4, 40, 40 );
timingsFullConvexityFastNonConvex<4>( R4, 20, 50 );
outputResults( 4, R4, "timings-fcf-convexity-ncvx-Z4.txt" );
}
return 0;
}
void getPoints(std::vector< Point > &pts) const
bool isFullyConvexFast(const PointRange &X) const
LatticePolytope CvxH(const PointRange &X) const
Definition: DigitalConvexity.h:522
bool isFullyConvex(const PointRange &X, bool convex0=false) const
PointRange envelope(const PointRange &Z, EnvelopeAlgorithm algo=EnvelopeAlgorithm::DIRECT) const
std::ostream & warning()
DGtal is the top-level namespace which contains all DGtal functions and types.
void timingsFullConvexityNonConvex(std::vector< std::tuple< std::size_t, double, bool > > &results, std::size_t nb_tries, std::size_t range)
Definition: pConvexity-benchmark.cpp:261
void timingsFullConvexity(std::vector< std::tuple< std::size_t, double, bool > > &results, std::size_t nb_tries, std::size_t nb_vertices, std::size_t range, double fconvexity_probability=0.5)
Definition: pConvexity-benchmark.cpp:122
void outputResults(Dimension dim, const std::vector< std::tuple< std::size_t, double, bool > > &results, const std::string &fname)
Definition: pConvexity-benchmark.cpp:343
void timingsPConvexityNonConvex(std::vector< std::tuple< std::size_t, double, bool > > &results, std::size_t nb_tries, std::size_t range)
Definition: pConvexity-benchmark.cpp:220
void timingsFullConvexityFast(std::vector< std::tuple< std::size_t, double, bool > > &results, std::size_t nb_tries, std::size_t nb_vertices, std::size_t range, double fconvexity_probability=0.5)
Definition: pConvexity-benchmark.cpp:170
void timingsPConvexity(std::vector< std::tuple< std::size_t, double, bool > > &results, std::size_t nb_tries, std::size_t nb_vertices, std::size_t range, double pconvexity_probability=0.5)
Definition: pConvexity-benchmark.cpp:74
void timingsFullConvexityFastNonConvex(std::vector< std::tuple< std::size_t, double, bool > > &results, std::size_t nb_tries, std::size_t range)
Definition: pConvexity-benchmark.cpp:303
srand(0)
